逆振り子ロボットに、いろいろな転倒をさせてみた。あるいは、転倒の回避を試みた。数え切れないほどやったが、その一部を書いておきたい。

逆振り子ロボットアイコメ01の雄姿(笑)は左のようなものだ。写真では、左右方向にだけ倒れるように作ってある。足先に向けて、2台のサーボのワイヤーが張ってあるので、これを張ったり緩めたりして転倒させたり、転倒を制御させたりしている。
写真は、サーボ角度をほぼニュートラルにちかい位置にして直立させている。
サーボを緩めて、自然転倒させた時の3軸加速度センサーが捉えるデータを示しておこう。
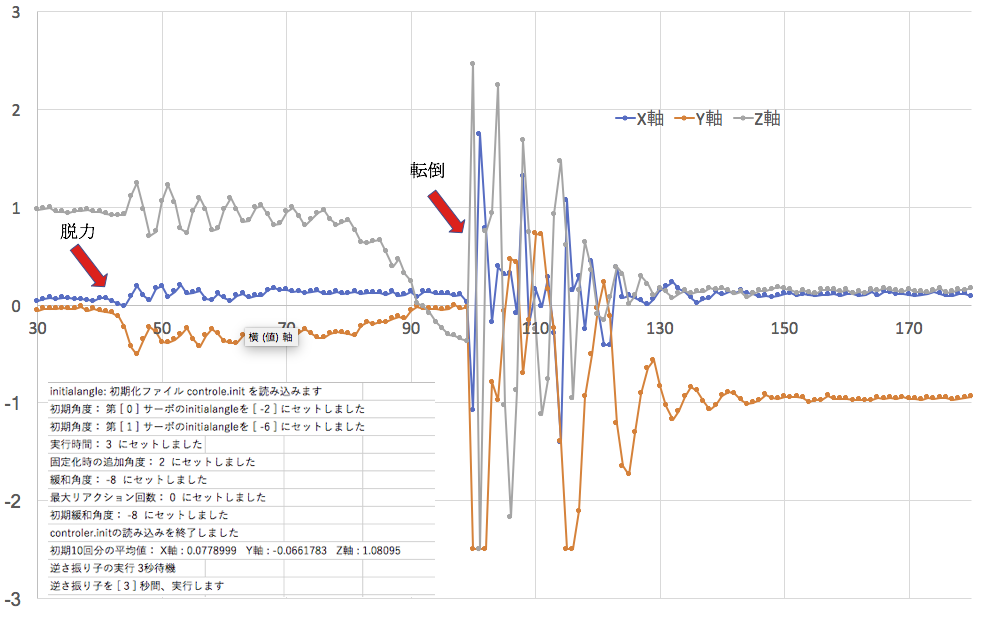
横軸の目盛りは10ミリ秒単位で、センサーから撮ってきたデータの番号である。縦軸は上から順に、Z、X、Y軸の加速度センサーのデータである。
Z軸は、垂直方向であるが、サーボの脱力によって上下の微妙な揺れが生じるが、倒れるに従ってそれは減衰している。青がX軸だが、倒れないようになっている方向のため、微妙な揺れだけにとどまっている。一番下のY軸のデータが、倒れる方向のものだ。ただ、ゼロから、一挙に(回転方向である負の方向に)上昇するが、倒れるに従ってまたゼロに戻っていっている。回転に従ってこの方向の動きがなくなるからである。倒れた瞬間に、加速度センサーはパニックになる。
このパニック状態は、ロボットが一番不快な状態になっていると考えれば良い。これは、のちに、ロボットに運動を学習させるときに、不快感のシグナルとして使いたいと思っている。
衝撃が治ると、Y軸が垂直になっているので、1g(gは重力加速度)になって、他はほぼゼロになっている。わずかの傾きがあるくらいだ。
次に、転倒をロボット自身んが検知した瞬間(0.1gの変化)、転倒する反対側のサーボを、角度を縮める形で固定した。すなわち、逆方向に揺り戻そうと動かした時の反応は、次のようになる。
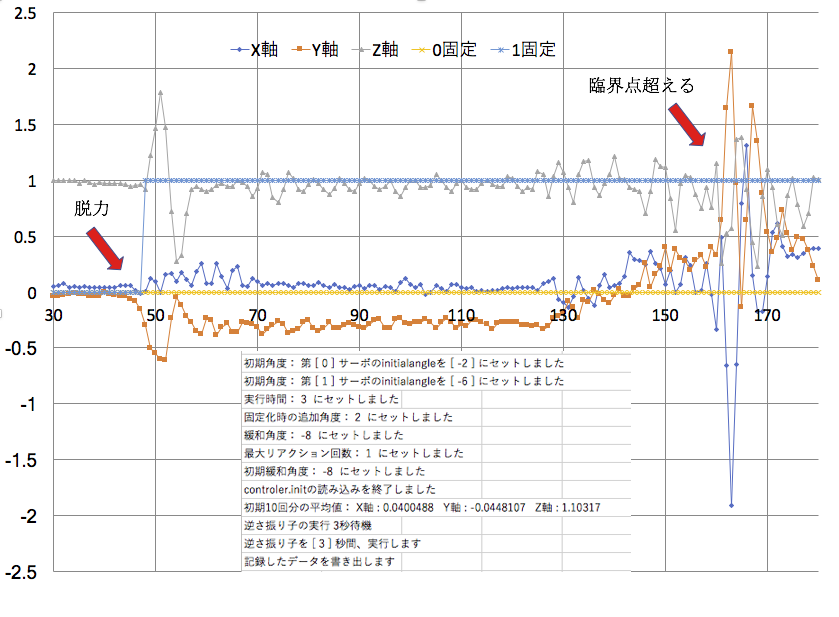 まず、Z軸が、脱力と片側固定化の、一瞬の大きな揺れの後、1gを維持している。先の完全転倒の場合と比べて、水平状態がほぼ維持されていることを意味している。それでもわずかに左に傾いていることは、Y軸の動きによって知ることができる。それが一見安定しているようだが、脱力から0.8秒後に反対側に向かっての回転が発生して、矢印のところで臨界点を超える。この臨界点を超えるというのは、データからの判断ではなく、ロボットを見ていた私が、これは、ほっておけば倒れると判断したところで、私がその時点でロボットを支えた。
まず、Z軸が、脱力と片側固定化の、一瞬の大きな揺れの後、1gを維持している。先の完全転倒の場合と比べて、水平状態がほぼ維持されていることを意味している。それでもわずかに左に傾いていることは、Y軸の動きによって知ることができる。それが一見安定しているようだが、脱力から0.8秒後に反対側に向かっての回転が発生して、矢印のところで臨界点を超える。この臨界点を超えるというのは、データからの判断ではなく、ロボットを見ていた私が、これは、ほっておけば倒れると判断したところで、私がその時点でロボットを支えた。
最初の転倒方向への完全転倒は避けれたのだが、逆のサーボが引き戻したことによって、逆側に倒れてしまう事態になったというわけである。
1関節ロボット上の加速度センサーデータ
(以下の記事の元になっているのは、この論文)
1関節ロボット、アイコメ0.1(外形はこちら)上におかれている3軸加速度センサーが転倒に対してどのように反応するかを調べてみた。
正直驚いた。ロボットに載せずに、机の上で動かしたりのシミュレーションはすでに行っていて、その結果も示しているが、その結果とは大きく違っている。
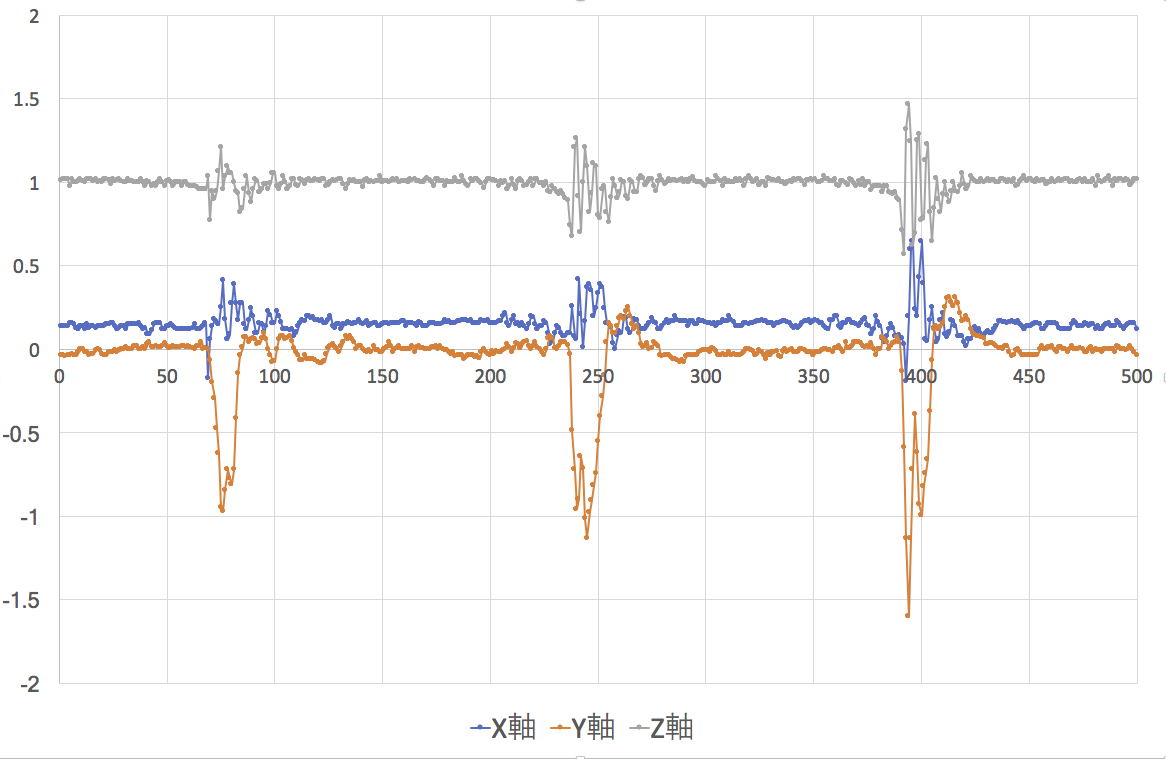 垂直に立てた状態から、手を離して、5度か10度自由に傾かせて、手で止めてまた垂直に戻すというのを3回やったデータである。止めたところは、およそ、ここで関節を固定させたらいいなと、私が判断した場所である。
垂直に立てた状態から、手を離して、5度か10度自由に傾かせて、手で止めてまた垂直に戻すというのを3回やったデータである。止めたところは、およそ、ここで関節を固定させたらいいなと、私が判断した場所である。
(1)重力の誤差が小さい。Z(縦)方向のg(重力加速度)は1で、他はゼロが理論的に予想されるところだ。ほぼ、そんな感じだ。Y軸は、私がほぼ水平(すなわち棒が垂直に立っている)と思われるように調整しているが、前後の軸(X軸)は、丁寧に調整していないのでわずかにずれている。
(2)一度の揺れを感度良く捉え、たくさんのデータを輩出している。前の結果と比べてもらえば一目瞭然だ。サーボによる調整のトリガを出す上で、とてもわかりやすい。
ここで、理論的に予測される、臨界角度を調べてみよう。アイコメ01は10センチの横棒の中央から33センチの高さ(コンピュータが置かれているアルミ板までの高さ使う)だから、その比は6.6である。この場合の臨界角βは、ラディアンで0.075869、角度で4.346973501度であることがわかっている(この論文参照)。
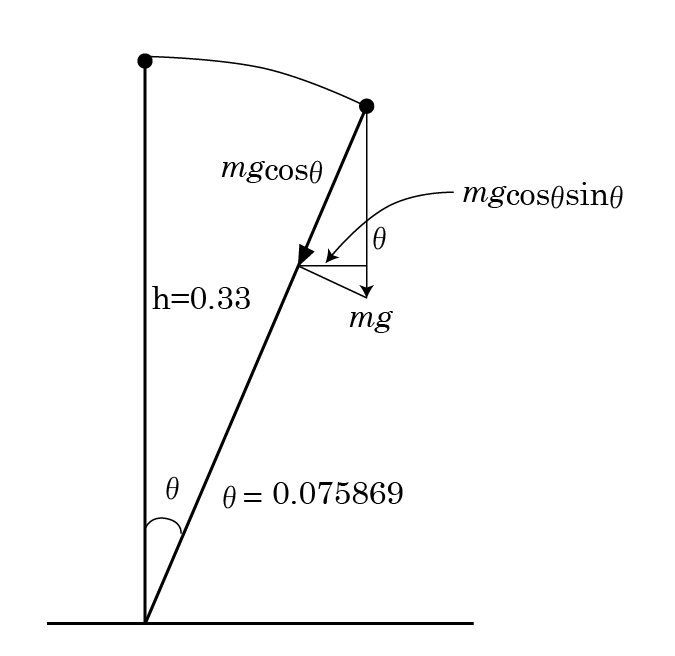
すると、左の図からわかるように、Y軸方向の加速度は、sinθcosθであるから、重力加速度のsinθcosθになったときが垂直からの角度がθになったときであることがわかる。このθに0.075869を入れると、上記の値は、0.001324162となる。つまり、Y軸方向の加速度が絶対値で、0.001324162ときである。
もし、この理論値が正しければ、極めて初期の段階で、関節の固定が必要となることを意味している。
サーボモータに、こんなに微妙なコントロールは不可能であるから、実際上は、センサーが倒れ始めているデータを出し始めた途端、関節を固定化するようにサーボの角度を与えることが必要になる。
1関節ロボットによる逆振り子理論の検証
(以下の記事の元になっているのは、この論文である)
早朝から、アルミの板と棒を切ったり穴開けたりしながら、この間議論してきた理論を実証すべく、自由な関節を1個だけ持ったロボットを作った。たくさんのボルトやナットを使ったが、一時期、電子工作に凝っていたので、その時のものでほとんど間に合わせた。
「冷蔵庫にあるものでラーメンを作った」という感じのロボットだ。
いや、「これはロボットではない」と言われればあえて否定しないが、自分では、私が自分で作った最初のロボットの筐体だと思っている。脳はあるが、まだ知恵は何も入っていない。あえて名前をつければ、AiComedian ver.0.1 である。アイコメと呼ぼうか。
 アルミの縦棒が机についているあたりに、アルミの横棒があり、それらをつないでいるのが横方向にだけ自由に回転する関節、ジョイントである。
アルミの縦棒が机についているあたりに、アルミの横棒があり、それらをつないでいるのが横方向にだけ自由に回転する関節、ジョイントである。
横棒には、前後に倒れないように4ミリのアルミ棒が左右に二本つけられている。だから、この縦棒は、左右にしか動かないのである。
ただし、今こうして立っているのは、上部に二つのサーボモータがついていて、下の横棒との間に0.3ミリのステンレス線が張ってあるからである。
さらにその上には、コンピュータ( RaspberryPi)と3軸加速度センサー、I2Cによるサーボコントローラを乗せたアルミの板がある。
サーボは、水平角度を0度として運用しているが、およそであって、今の状態は、手前のサーボ(1番)がサーボの角度で0度、向かいのサーボ(0番)がサーボの角度で+3度でほぼ釣り合った状態になっている。サーボの角度を下向きに変化させると、縦棒は勢いよく倒れる。
C++で加速度センサーとサーボをコントロールするクラスを、それぞれに作ってあるので、センサーの検出した傾きから、サーボをコントロールして、逆さ振り子の状態を実際に創り出したいと思っている。
ことの成否は、転倒開始時に、加速度センサーがどんなデータを送ってくるかにかかっている。
加速度センサーの精度
(以下の記事の元になっているのは、この論文)
ロボットの転倒に関する議論をしてきたが、逆振り子で転倒を回避する場合でも、自らの傾き、ないしは揺らぎを捉えることが不可欠である。ここでは、KXSD9-2050という750円のセンサーを使っているので、どこまで精度が出るのかがいたって不安である。
そこで、より詳細に調べてみた。
KXSD9-2050については、sensitivityを819counts/g (g: 重力加速度 = 9.80665 m / s2)に変更したことを除いて、初期設定を採用している。
10ミリ秒に一つのデータを取る計算で、500個のデータを取った。その間に、センサー(RaspberryPiに固定している)を6回だけ、数ミリずらせる速度をY軸方向に与えた。そのうちの50個目から200個目までのデータを図で表したものが以下の画像である。
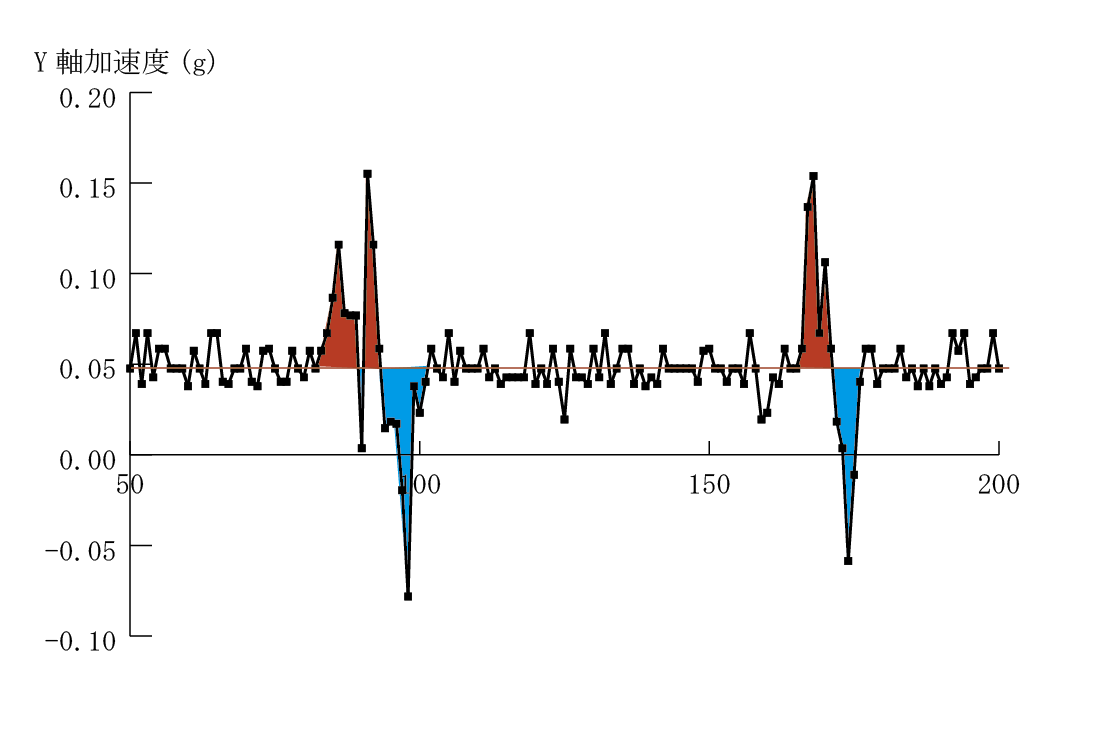 Y軸だけをみている。縦軸のgはY軸方向の重力加速度である。水平方向であるから0でなければならないが、0.05となっているのは、多少Y軸が傾いていることからくるのか、私の家が傾いているのか、机が傾いているのか、そんなところだろう。ホワイトノイズとして処理する。
Y軸だけをみている。縦軸のgはY軸方向の重力加速度である。水平方向であるから0でなければならないが、0.05となっているのは、多少Y軸が傾いていることからくるのか、私の家が傾いているのか、机が傾いているのか、そんなところだろう。ホワイトノイズとして処理する。
数ミリ動かしたことによる影響は、赤と青で色ぬりされた部分に現れている。赤から始まっているのは、Y軸のプラスの方向に加速度が与えられ、マイナスになっているのは、速度が低下して、ほぼ再び止まったことを表している。止まったということは、赤の面積と青の面積がほぼ等しいことを表す。
実際移動した距離は加速度がプラスから始まっているので、Y軸方向に移動してどこかで止まったということで、それまでのプラスの距離になる。
指で数ミリ動かしただけで、これだけのものがとらえられることは、この安物のセンサーも結構使える可能性があることを示している。
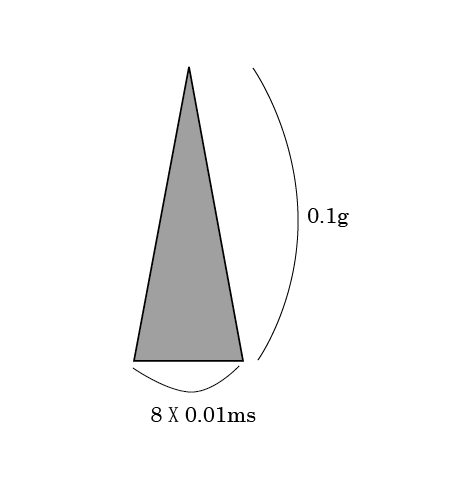 今、赤と青の部分が単純な三角形だったとしよう。横幅が8目盛、高さが0.1gくらいになる。この時、最高速度は、
今、赤と青の部分が単純な三角形だったとしよう。横幅が8目盛、高さが0.1gくらいになる。この時、最高速度は、
80(ms)X0.1(g)X(1/2)=0.08X0.1X0.5X9.80665=0.039226(m/s)
およそ1秒間に4センチ動くくらいの速度が最高速度だったということになる。
それから速度が0になるまで同じくらいの時間がかかったとしよう。簡単化のために、全て、三角形で捉えよう。(実際は曲線)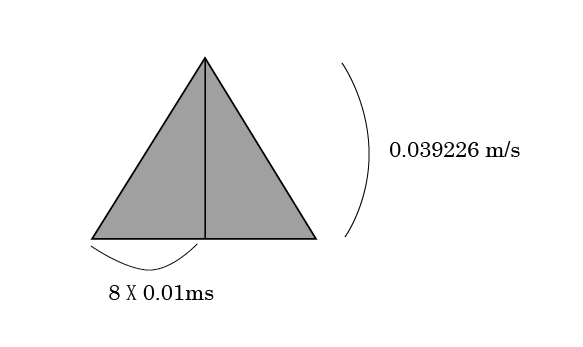
そうすると、移動した距離は、
0.08X2X0.039226/2=0.00313808(m)
すなわち、3.2ミリ移動したことになる。私が先に数ミリ動かしたと言ったが、ほぼその値に一致する。
ということは、この加速度センサーが捉えている加速度は、ノイズできなものはありながらも、なかなか、実態を反映しているということなのである。
逆さ振り子としてのロボット
以下の記事についての詳細は論文参照
NAOは、ただ立っているとき、小さく体を揺らしている。これはALDEBALANの技術者が、より生きているように見せようとした工夫だろう。実際そう見える。ただこれが、NAO自身にとって必要なこととは思えない。問題は、なぜ体を揺らすことが生きているように見えるために必要なのかということだ。結局それは、人もまた、立っている時でも体を微妙に揺らせているからだ。人の場合は、体を揺らせることによって直立状態を維持できる、という必要においてそうなのだ。無意識に体の姿勢を制御している。
この揺らせることによって直立を維持するメカニズムの基本的なところは理論モデルとシミュレーションで示してきた。
理論モデルで示したように、直立構造の運動方程式は、単振り子の運動方程式とよく似ている。同じように見える。ただ、加速度の方向が逆向きになっていて、三角関数ではなく指数関数でそれが解けるようになっている。
下向きのたん振り子は、それ自体に、あるいは内生的に、復元力が働くのだが、逆さまの振り子であるロボットは(現在の多くのロボットは、NAOも含めて逆さ振り子とは言えない。新しい設計思想で作られるロボットのことを意味する)、それ自体は、転倒が基本なのだ。それに対する外生的な揺り戻しが生じることによって転倒を微妙に避けている。このような姿勢制御によって、直立が維持される。そのプロセスは、結局、揺れている状態と同じになるのだ。
この揺れは、この立っている状態に冗長性を生むというもう一つの、とても大事な側面を持っている。単なる剛体であれば、ちょっとした撹乱としての傾きで倒れてしまう。しかし、常に揺れながら状態を直して入れば、撹乱を吸収できるゆとりが出てくる。
スポーツでは、膝や腰や腕を柔軟に使うことが大切なこととして求められる。人間のさまざまなしなやかさは、関節の自由度の大きさによって確保されている。
そのようなロボットをイメージすることがとても大切だ。
時間を入れたシミュレーション
ロボットの転倒とその回避に関わる分析で、これまでは明示的に時間が入らなかった。そこで、ロボットの転倒と回復に関する運動方程式を求めてシミュレーションしてみた。
結果の詳細は論文参照
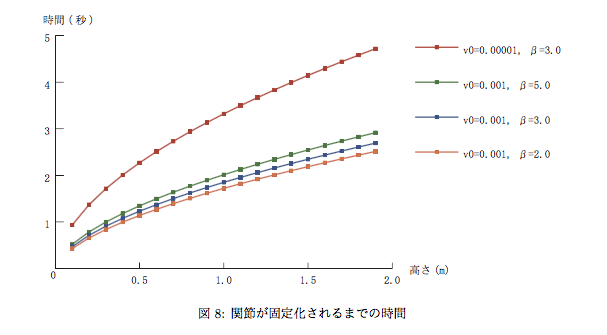
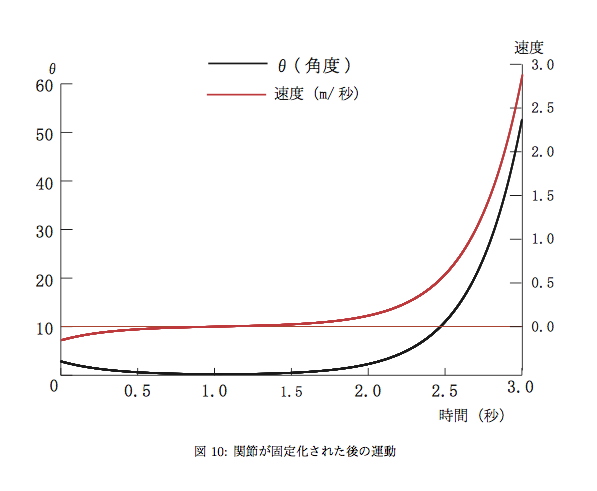
ロボット転倒問題のシミュレーション解
前の記事で書いたロボットが倒れる、倒れない問題について、シミュレーション解を出すことができた。なお、計算に使ったJAVAの関数は、以下の論文の中に示しておいた。
(詳細は論文参照)
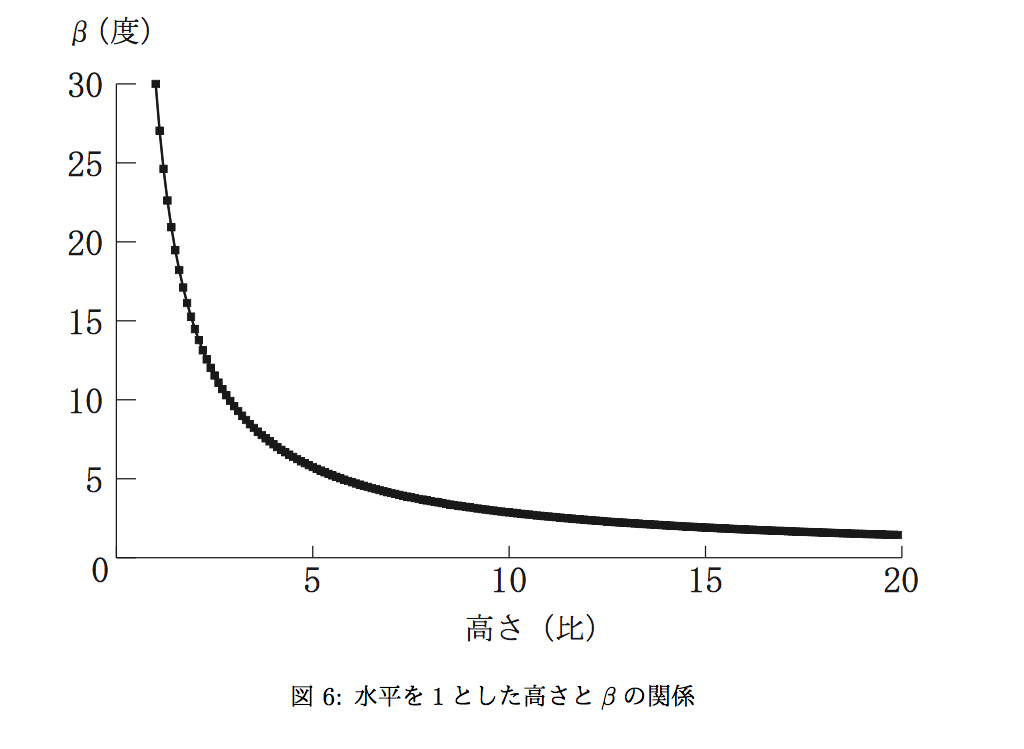 この図で、横軸は、横の棒の長さを1としたときの高さである。縦軸が、転倒を回避するために、臨界点で止まる(再び位置エネルギーが元の値に戻る)ために必要な関節を固定化する角度である。ラディアンから度に変換している。
この図で、横軸は、横の棒の長さを1としたときの高さである。縦軸が、転倒を回避するために、臨界点で止まる(再び位置エネルギーが元の値に戻る)ために必要な関節を固定化する角度である。ラディアンから度に変換している。
計算結果の誤差は、ここで解とみなした値のときで、高さの比が1のときが最も小さく0.0000000082である。高さの比がここで調べた中で最も大きい20.0のときに0.0000011608である。いずれもゼロに極めて近く、ほぼ解であると考えて間違いないだろう。刻み方をもっと細かくすれば、さらに誤差を小さくできることが予想される。ただ、高さが高くなるほど誤差は僅かながら大きくなっている。その理由は、高さが高いと、微妙なバランスが求められると考えても良いだろう。
その結果の特徴は、まず、理由はまだ正直わからないのだが、常にαとβは等しくなる。
高さが1のとき、すなわち、横棒と縦棒が同じとき、角度は29.99697622度、ほぼ30度だ。何か理由がありそうな角度である。αも同じになることは先に述べておいた。綺麗に90度を三等分する角度になっている。ただ、この角度は大きい。つまり、頂点で手を離して、30度傾くまで、自由な関節の回転を放置しておいて良いのだ。その後固定化すると、ギリギリ転倒を回避できる。高さが低いからである。
小さなロボットが転倒しにくい理由はここにある。
また、比率で見た高さが高くなると、最初は急速に関節を固定化するまでの角度が小さくなっている。その後は、少しずつ低下する。すなわち、高さが高くなればなるほど、転倒しないために関節を固定化しなければならないタイミングは早くなるのである。僅かに傾いたら、即固定化ということになっていく。
それでも、高さが10のときに、β=2.870976923度、ほぼ3度の余裕がある。3度傾いたら、関節を固定化しなければならないのである。高いと、微妙な調整が必要になる。
これだけでも面白い結果だが、人に応用するともっと興味深い。例えば、私の身長は182cmである。一方、足のくるぶしの関節から足のつま先までの長さは18cmくらいである。高さの比は、10.1である。
上の計算で、10.1の限界度、βは、2.843990611度である。つまり、足前に出したりせずに、動かさずに立った状態を維持するためには、2.8度、前に傾いたら筋肉を緊張させなければならないのである。
確かに、体を前にわずかに倒そうとすると筋肉を硬直させるが、この角度が、2.8度だよとこのシミュレーション結果は示している。もちろん、人間の体は質量が分布しているので、理論モデルで示したような質量の一点集中とは違っている。
一つ首をかしげることは、常にαとβが、ぴったり等しくなることである。数学モデルから、解析的に言えそうなのだが今の所わからない。
残された課題は、(1)頂点から倒れ始めて、関節が固定され、最終的に転倒の臨界角度に至るまでの時間を示すことである。確かに、高さが高いほど、関節を固定しなければならなくなるまでの角度は急速に小さくなっていく。しかし、そこに至る時間はどうなるかわからない。それを解析に出せないかを考えることである。また、その時間には、B点の質量が影響を与える可能性が高い。メトロノームが重りを上に持っていけばいくほど、スピードが遅くなることも考慮される。(2)実際にシステムを組んでシミュレーションして確かめることである。シミュレーションするための材料はほぼ整っている。加速度センサーも、サーボも、RaspberryPiから制御できるようになっているからである。
ロボットの転倒及び転倒回避に関する基本問題
昨日、ロボットが「倒れる、倒れない、倒さない問題」と言うのを考えたと、その内容をここに書いた。答えは出ていなかった。
今日、ちょっと昼寝をして起きたら、答えを思いついたので、メモを書いた。間違いを見つけたら、教えていただきたい。
この問題とそのシミュレーション解については、こちらの記事に詳細を示しておいた。論文もダウンロードできる。

3D加速度センサーのKXSD9-2050をRaspberryPi 3 から使う
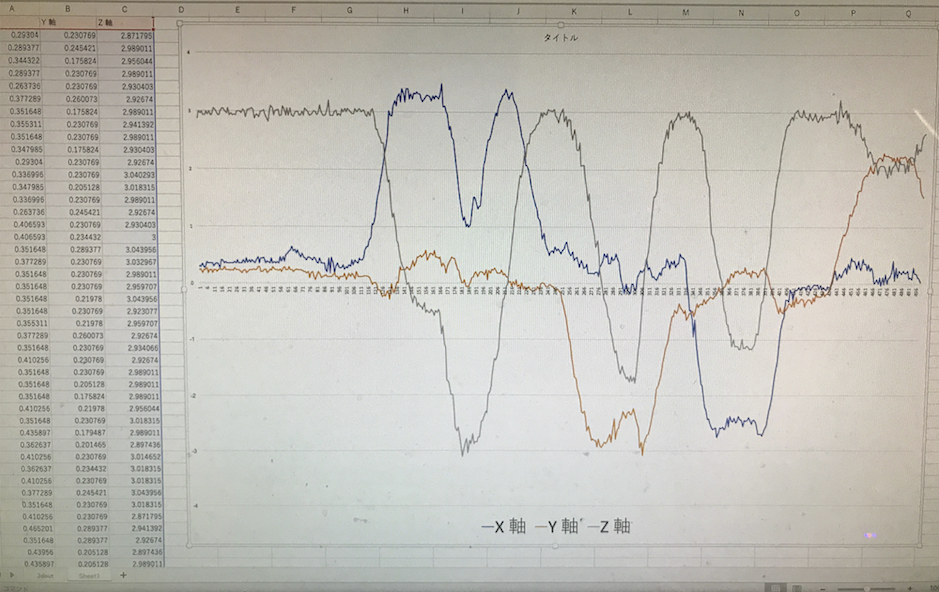 3D加速度センサーのデータの拾い方に苦労したが、これでいいのかもしれないというところまで来たので、記録しておこう。
3D加速度センサーのデータの拾い方に苦労したが、これでいいのかもしれないというところまで来たので、記録しておこう。
加速度センサーを起動して、500回分ループ動かした(データを取得した)。1データ100m秒間隔でとっている。
まず、水平においている。縦が、Z軸だから、重力がかかっているので、1gのはずだが、3gになっているのは、測定レンジを6gにしてあるからなのかもしれないがよくわかっていない。確かに、裏返すと-1gで、3gだと-3gで結局幅が6gになるので、それでいいのかもしれない。
まず、X軸に向かって回転しながら、裏返すところまで持って行った。途中ちょっとフラフラした分も描かれているが、Z軸がマイナスに触れた分、X軸に重力がかかっている。次に、Y軸に沿ってマイナス側に回転させたら、確かにY軸はマイナスに触れている。その後、X軸とY軸をそれまでの操作と逆方向に回転させた。図はほぼそれを忠実に再現している。
モジュールのつなぎ方を記録しておく。

モジュールは、KXSD9-2050(画像の右下)だ。RaspberryPi(画像では、下にあるものだが、ボードを1枚被せて、電源5V、電源3.3V、I2Cの拡張コネクタを乗せている)とI2C(アイスクエアシーと発音する)で接続する。
ピン接続は以下の通りだ。
モジュール1→電源3.3V+(新しく5Vから降圧したピンに、Raspberryからとっても良い)
モジュール2→電源のGNDー
モジュール5→RaspberryPiのSCL、GPIO3
モジュール6→電源3.3V+(これをつながないと、I2Cがうまく機能しない)
モジュール7→RaspberryPiのSDA、GPIO2
以上だ。3.3Vを二つ繋がなければならないのが気をつける点だ。
繋いだら、RaspberryPiのターミナルで
i2cdetect -y 1
と打って、モジュールのアドレスを確認しておく。
$ i2cdetect -y 1
0 1 2 3 4 5 6 7 8 9 a b c d e f
00: -- -- -- -- -- -- -- -- -- -- -- -- --
10: -- -- -- -- -- -- -- -- 18 -- -- -- -- -- -- --
20: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
30: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
40: 40 -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
50: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
60: -- -- -- -- -- -- -- -- -- -- -- -- -- -- -- --
70: 70 -- -- -- -- -- -- --
サーボモータ関係のものが二つ繋がっているが、モジュールのアドレスは、0x18となる。
プログラムは、
#include <stdio.h>
#include <wiringPi.h>
#include <wiringPiI2C.h>
// コンパイル
// gcc 3dsensor.c -o 3dsensor -lwiringPi
int main(int argc, char **argv)
{
int i2c_fd; // I2Cデバイスファイル
// sudo i2cdetect -y 1 を実行すればKXSD9-2050のI2Cアドレスを知ることができる
int i2cAddress = 0x18; // KXSD9-2050のI2Cアドレス
int i;
int xregH,xregL,xout;
int yregH,yregL,yout;
int zregH,zregL,zout;
double xac,yac,zac;
// I2Cデバイスファイルをオープン
i2c_fd = wiringPiI2CSetup(i2cAddress);
// KXSD9-2050 イニシャライズ
if((wiringPiI2CWriteReg8(i2c_fd,0x0a,0xca)) < 0){
printf("write error register 0x0a: KXSD9-2050 イニシャライズに失敗\n");
return 1;
}
printf("write register:0x0a = 0xca\n");
// WiringPi イニシャライズ
if(wiringPiSetupGpio() == -1){
printf("WiringPi イニシャライズに失敗\n");
return 1;
}
// 加速度データを取得
printf("データを500個取得します\n");
for(i=0; i<500; i++){
// デバイスからデータ取得
xregH = wiringPiI2CReadReg8(i2c_fd,0x00);
xregL = wiringPiI2CReadReg8(i2c_fd,0x01);
xout = xregH<<4|xregL>>4;
//printf("xH: %6d xL: %6d\n",xregH,xregL);
yregH = wiringPiI2CReadReg8(i2c_fd,0x02);
yregL = wiringPiI2CReadReg8(i2c_fd,0x03);
yout = yregH<<4|yregL>>4;
//printf("yH: %6d yL: %6d\n",yregH,yregL);
zregH = wiringPiI2CReadReg8(i2c_fd,0x04);
zregL = wiringPiI2CReadReg8(i2c_fd,0x05);
zout = zregH<<4|zregL>>4;
//printf("xH: %6d xL: %6d\n",xregH,xregL);
xac = (double)(xout-2048)/(double)273;
yac = (double)(yout-2048)/(double)273;
zac = (double)(zout-2048)/(double)273;
//printf("X軸 : %6d Y軸 : %6d Z軸 : %6d\n",xout,yout,zout);
printf("No. %4d : X軸:%6d Y軸:%6d Z軸:%6d ==>> X軸:%10.6f Y軸:%10.6f Z軸:%10.6f\n",i,xout,yout,zout,xac,yac,zac);
delay(100);
}
return 0;
}
指定したアドレス(仕様書に書いてある)から、データを取得できる。ただ、2バイトで送られてくる。そのうちのHighとLowから、12ビットが使われるのがちょっと面倒。そこで、取得したデータの、Highを4ビットだけ左にシフトさせ、Lowを逆に4ビット右に論理和をとったものをデータとしている。
操作のイメージは次のようになる。有効なビットをA、無効なビットをX、ゼロは0で表そう。
まず、Highは AAAAAAAAを左に4ビットシフトさせてAAAAAAAA0000とする。
次にLowはもともとAAAAXXXXとなっているので、右に4ビットシフトさせて0000AAAAとするわけである。
上記二つの値の論理和をとると、
AAAAAAAAAAAA
と見事に12ビットになるという手筈なのだが、これでいいかどうか確証はない。
このデータから元の加速度を出す方法も大事だ。プログラムの中に書かれているようにやればいいはずだ。まず、オフセット値が与えられている。ここの場合、2048カウントである。得られたデータとこのオフセット値の差をとって、その差を1gあたりのカウント値 (6g幅を使用している場合(デフォルト)は273)で割ることによってgの値が取れるはずなのだ。これも、誰かに確かめているわけではないが、論理的にはそうなるということだ。
これで計算したものが、冒頭の図である。図がほぼそんな感じなので、間違っていないと思う。
なお、プログラム始めの
KXSD9-2050 イニシャライズ
は、マニュアルによると、電源起動時にやっているようなのだが、念のためにやっておいた。
倒れる、倒れない、倒さないの問題
以下の問題については、そのシミュレーション会も含めてこちらの記事に詳細が書いてある。
ロボットが倒れる、倒れない、倒さないという問題について、解いてはいないが、問題だけをまず考えた。

手書きの図で申し訳ないが、見ていただきたい。今、CDという棒と、AEという棒が、A点で関節のようにつながっていると考えてください。図(1)。2次元で考えます。関節は、A点を支点に自由に動くこともできるし、固定化することもできると考える。A点の位置を変えることはできない。人間の足首の関節だと考えてもらって良い。
縦の棒の、Bの位置に、m( > 0)という正の重さの塊があります。簡単化のために、この塊以外は重さがない。棒も、剛体だけれど「重さがない」と考えてください。
今、縦棒が水平からの角度θのところで、関節Aを固定し、つまりCDの棒とAEの棒をそれ以上動かないように固定化したとして、このθをある限界を超えて、小さなところで固定すれば、これは右回転して倒れてしまうだろう。その限界のθは、計算しなくても、BがちょうどDの真上に来る時であることが想像つく。つまり、図(2)のような状況である。何しろ、棒には重さがないのだから。(B点がD点の真上よりも右側になれば倒れる)
逆に、BがDの真上より左側で、関節が固定されれば、復元力が働くだろうことも、計算するまでもない。つまり、右側には倒れない。
解けると思うが解いていない問題はここからだ。
今、縦棒が、D点の真上に来るまで、自由に動く関節Aの元で、動きながら到達し、急に関節を固定化させたら、あるいは固定化させたとしても、当然、それまでの運動量があるから、慣性の法則か何かわからないけれど、右回転でこのシステムは倒れてしまうだろう。
ちょっと言い換えれば、頂点から少し右側に外れたところで重りから手を離して自由にさせた状況で、D点で急ブレーキで固定しても、倒れるということである。
今、頂点の極近くで重りから手を離したら、D点で、固定化させても倒れたとする。一方、D点の真上で手を離して、そのままD点で固定したら、先の洞察と同じようにそれは微妙に倒れないだろう。
だとすると、固定化するのをD点の真上よりも、もう少し早く固定化させれば復元力が優って、右側に倒れ込まないところがあるのではないか、これが問題。なぜなら、D点の真上よりも早く固定化すると、固定化したために、D点を軸に回転する動きが発生し、それによって重りがそうでない場合よりも上に持ち上げられて、そのこと(位置エネルギーの増加)のためにエネルギーが使われて、運動が減速されて元に戻る力が買ってしまうのではないかということである。
図(4)にその状況を書いている。角度が元よりも大きめのθ''のところで固定化したために、Dを新たな回転軸としてδの角度が発生し、重りBが少し持ち上がりながら回転することになって、復元力が発生するのではないかということである。
問題は、復元力が発生する限界の固定化点はどこかということである。
基本、これが、人間のする、倒れないための復元努力に近いと思っている。
数学的にというか、物理学的に解いてみたい。高校の物理で溶けるだろうと思うのだが。