ディープラーニングの自己符号化手法で、入力層はピクセル数の784、隠れ層を順に、600、400,300、出力層は数字の0から9に対応させて10ユニットというネットワークの学習とテストをしたら識字率は、96%になった。これまでのをまとめると
| モデル | 隠れ層 | 確信度(正解ユニットの出力が0.8以上のデータ数) | 正解率(%) | 学習法 |
| A | 400 | 8435 | 93.1 | 通常 |
| B | 300-150 | 8557 | 94.13 | 自己符号化 |
| C | 600-300-150 | 7848 | 89.37 | 自己符号化 |
| D | 600-300-150-50 | 7893 | 90.06 | 自己符号化 |
| E | 600-400-300 | 8953 | 96.04 | 自己符号化 |
この確信度について説明しておこう。認識した数字は、最終層の10ニューロンのどれが発火しているかで判断するが、成果率は、単に一番出力値の大きなニューロンを選んでいる。例えば、他の九個のニューロンが0.1以下の値で、8番目のニューロンが0.15でも、これは8と認識したとしてそれが正解ならば正解としているのである。
そうではなくて、その出力ニューロンの発火を0.8以上の値を出していない限り発火と認めないとした場合の正解数を確信度としている。
すると、この確信度でもモデルEのパフォーマンスが最も高い。つまり正解率でも96%と最も高いが、0.8以上の発火に限定しても、ほぼ90%の正解率になる。
ただ、一月になるのは、このモデルE以外の自己符号化は、各層の自己符号化の学習で、36万回の学習をやらせて、やや過学習になったのかもしれないと思っている。モデルEは、データ数の60000回で、各層の事前学習もやめている。
その辺りのこともこれから確認したい。
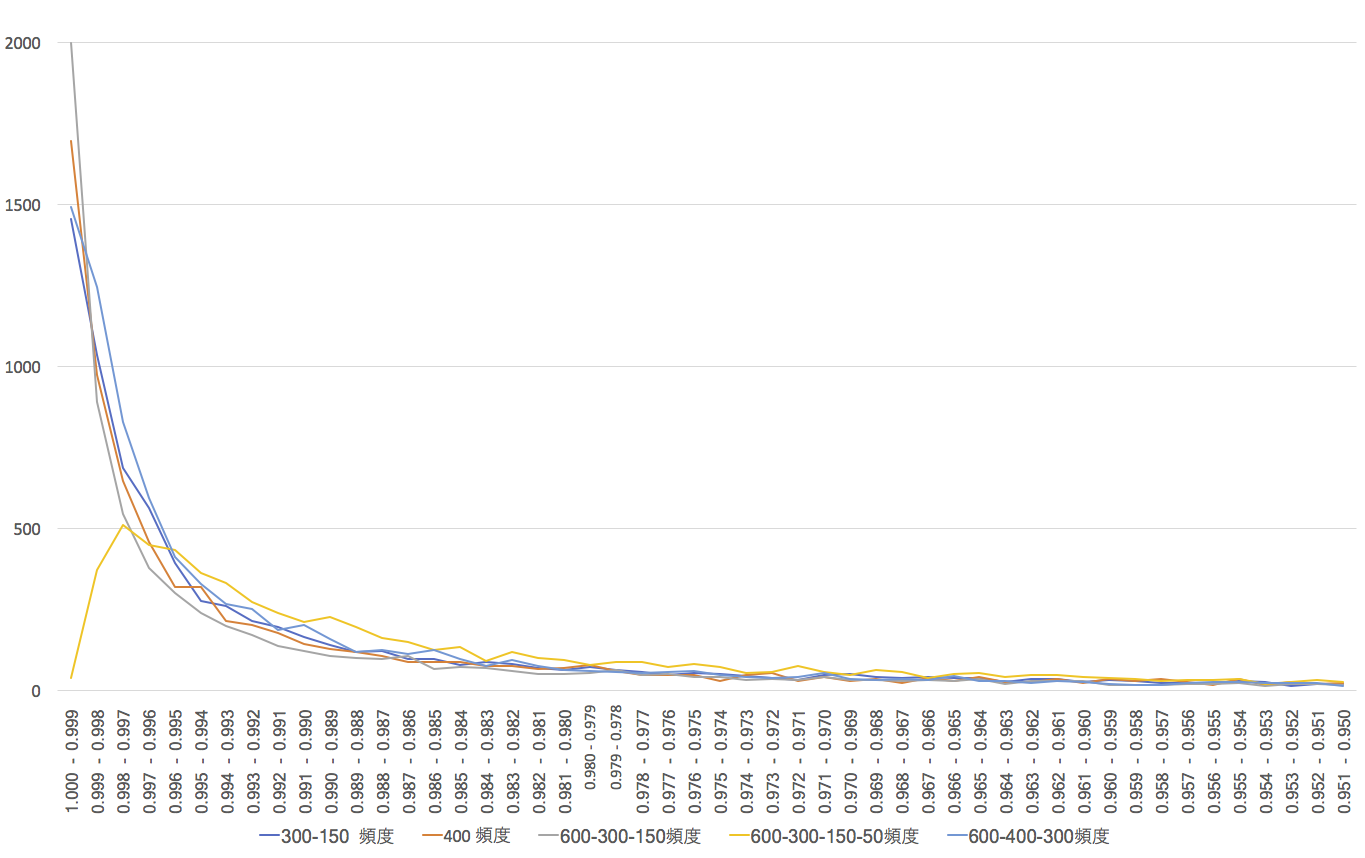
正解ニューロンの発火出力ごとのヒストグラムは以下のようになっている。発火値が0.95以上のものをあげているが、ほとんどの正解が高い発火度で実現しているのは確認できるだろう。