日別: 2017年6月5日

オートエンコーダーなどのディープラーニングをマルチスレッド化してみたが、少しも速くならなかった。レイヤーにあるニューロンの出力計算やDeltaの計算をスレッドに分散させてみたのだが、それだけでは速くならないどころか、微妙に遅くなっている（笑）
スレッド化のオーバーヘッドが、そのメリットを上回っているのだと思われる。マルチスレッドの入れ方も悪いかもしれない。今の状態で十分速いと理解すべきだろう。当面、手を出さない。

オートエンコーダーなどのディープラーニングは、元のニューラルネットワークが、勾配喪失や過学習の問題で行き詰ってしまったのを打ち破ったものだった。実際、私も、その有効性を確認できた。ただ、ひとつひとつの隠れ層の事前学習を過剰にやると、問題も起こってくることもわかった。
例えば、先の記事にも書いたが、入力層と出力層以外に、隠れ層の数を3層にして、それぞれのニューロン数を600、400、300にして、隠れ層の事前学習も、60000個の文字を一通りやるだけにする。すると、事前学習は収束しないのだが、Autoencoderののちに実施したテストでは、96％の正解率に上昇した。しかし、これで、各隠れ層の事前学習を収束するまで徹底的にやるとどうなるか。ここでは、ひとつの層を通常6万回のところを、それをさらに六回繰り返して、36万回データを使って事前学習させたら、正解率が88.7%まで落ちてしまったのだ。
これだと、ああ、事前学習も過学習に陥るのだな、ということになる。
しかし、実はそう単純なことではないのだ。そのことを見るために次の図を示す。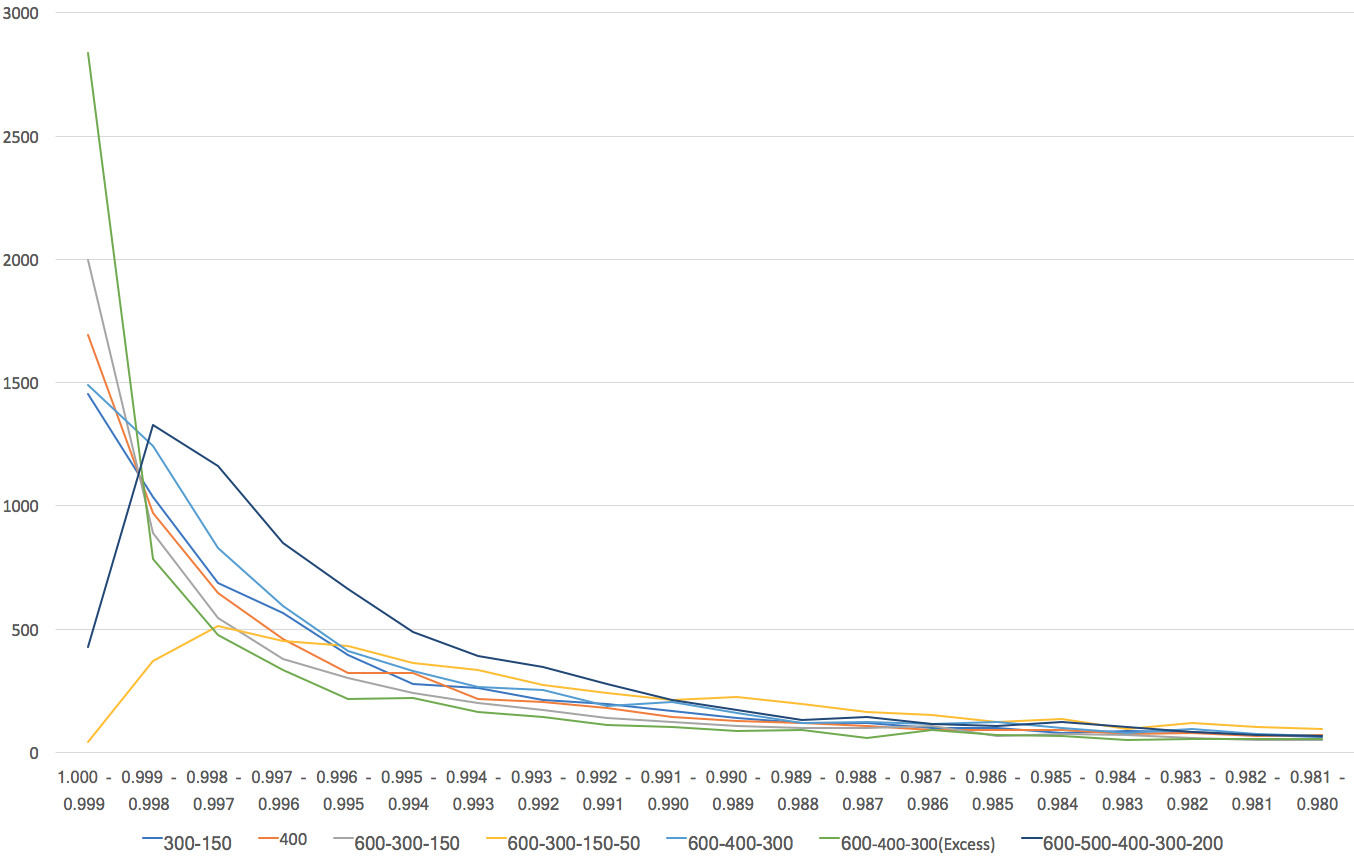
この図で、緑色の線が、Autoencoderで過度に学習させた先のネットワークだ。驚くべきことに、正解した出力ユニットの出力値が3000近くが0.999以上（最大値は1.0）で出力しているのだ。
つまり、自分が正しいと判定したことに強い確信を持っているということだ。あるいは、せいか率を犠牲にしても、そういう確信を持ちたがるネットワークだと言って良い。これに対して、過度に学習させなかったものは、正解率は高いが、だいたいそうだろう、という感じで答えを出してきていることがわかる。
結局、ネットワークに個性が出てきたのだ。正解ということに確信を持ちたいというネットワークと、いやいや、だいたいそうだろうと答えるタイプのネットワークが現れたことになる。
問題は、応用の場合、ロボットの小脳としてどちらのタイプのネットワークを使うべきかということだ。

ディープラーニングの自己符号化手法で、入力層はピクセル数の784、隠れ層を順に、600、400，300、出力層は数字の0から9に対応させて10ユニットというネットワークの学習とテストをしたら識字率は、96%になった。これまでのをまとめると

モデル	隠れ層	確信度（正解ユニットの出力が0.8以上のデータ数）	正解率（％）	学習法
A	400	8435	93.1	通常
B	300-150	8557	94.13	自己符号化
C	600-300-150	7848	89.37	自己符号化
D	600-300-150-50	7893	90.06	自己符号化
E	600-400-300	8953	96.04	自己符号化

この確信度について説明しておこう。認識した数字は、最終層の10ニューロンのどれが発火しているかで判断するが、成果率は、単に一番出力値の大きなニューロンを選んでいる。例えば、他の九個のニューロンが0.1以下の値で、8番目のニューロンが0.15でも、これは8と認識したとしてそれが正解ならば正解としているのである。
そうではなくて、その出力ニューロンの発火を0.8以上の値を出していない限り発火と認めないとした場合の正解数を確信度としている。
すると、この確信度でもモデルEのパフォーマンスが最も高い。つまり正解率でも96％と最も高いが、0.8以上の発火に限定しても、ほぼ90％の正解率になる。
ただ、一月になるのは、このモデルE以外の自己符号化は、各層の自己符号化の学習で、36万回の学習をやらせて、やや過学習になったのかもしれないと思っている。モデルEは、データ数の60000回で、各層の事前学習もやめている。
その辺りのこともこれから確認したい。
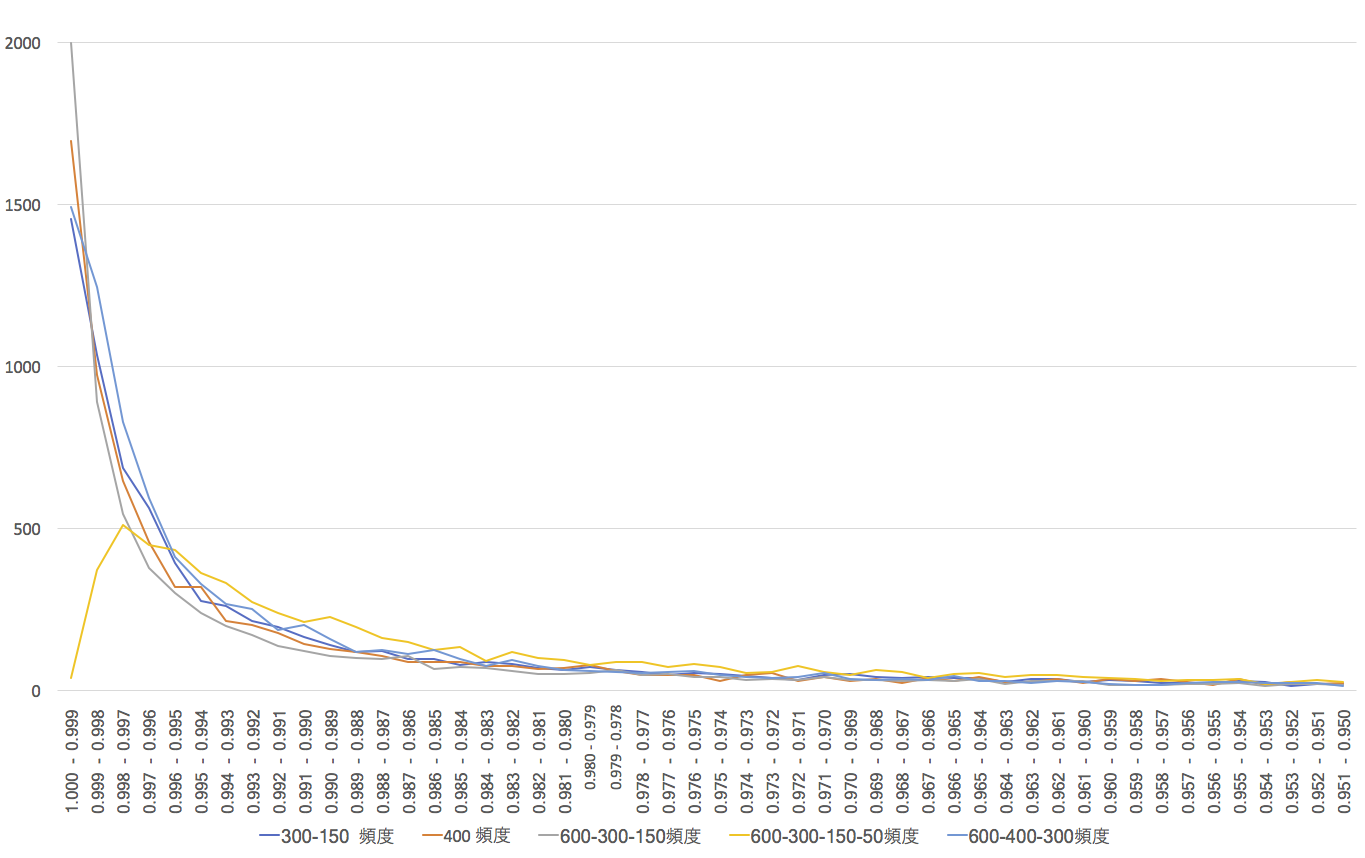
正解ニューロンの発火出力ごとのヒストグラムは以下のようになっている。発火値が0.95以上のものをあげているが、ほとんどの正解が高い発火度で実現しているのは確認できるだろう。