（以下の記事の元になっているのは、この論文）
ロボットの転倒に関する議論をしてきたが、逆振り子で転倒を回避する場合でも、自らの傾き、ないしは揺らぎを捉えることが不可欠である。ここでは、KXSD9-2050という750円のセンサーを使っているので、どこまで精度が出るのかがいたって不安である。
そこで、より詳細に調べてみた。
KXSD9-2050については、sensitivityを819counts/g （g: 重力加速度 = 9.80665 m / s2）に変更したことを除いて、初期設定を採用している。
10ミリ秒に一つのデータを取る計算で、500個のデータを取った。その間に、センサー（RaspberryPiに固定している）を6回だけ、数ミリずらせる速度をY軸方向に与えた。そのうちの50個目から200個目までのデータを図で表したものが以下の画像である。
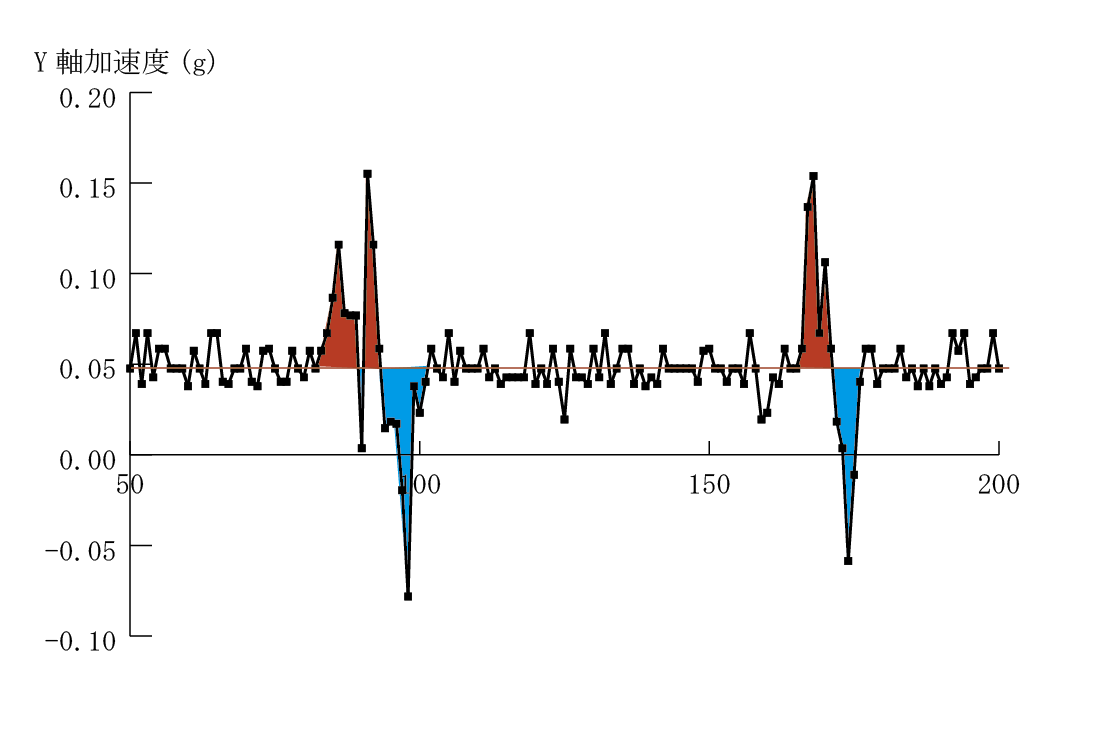Y軸だけをみている。縦軸のgはY軸方向の重力加速度である。水平方向であるから0でなければならないが、0.05となっているのは、多少Y軸が傾いていることからくるのか、私の家が傾いているのか、机が傾いているのか、そんなところだろう。ホワイトノイズとして処理する。
数ミリ動かしたことによる影響は、赤と青で色ぬりされた部分に現れている。赤から始まっているのは、Y軸のプラスの方向に加速度が与えられ、マイナスになっているのは、速度が低下して、ほぼ再び止まったことを表している。止まったということは、赤の面積と青の面積がほぼ等しいことを表す。
実際移動した距離は加速度がプラスから始まっているので、Y軸方向に移動してどこかで止まったということで、それまでのプラスの距離になる。
指で数ミリ動かしただけで、これだけのものがとらえられることは、この安物のセンサーも結構使える可能性があることを示している。
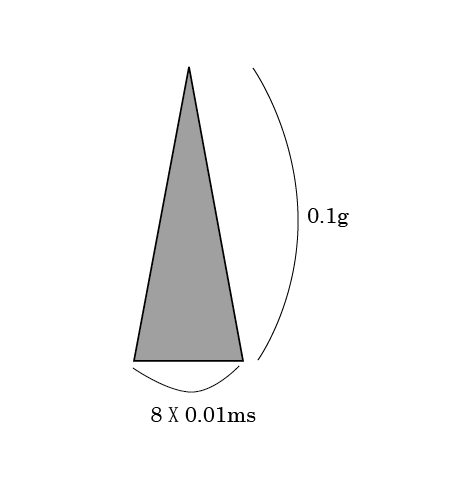今、赤と青の部分が単純な三角形だったとしよう。横幅が8目盛、高さが0.1gくらいになる。この時、最高速度は、
80(ms)X0.1(g)X(1/2)=0.08X0.1X0.5X9.80665=0.039226(m/s)
およそ1秒間に4センチ動くくらいの速度が最高速度だったということになる。
それから速度が0になるまで同じくらいの時間がかかったとしよう。簡単化のために、全て、三角形で捉えよう。（実際は曲線）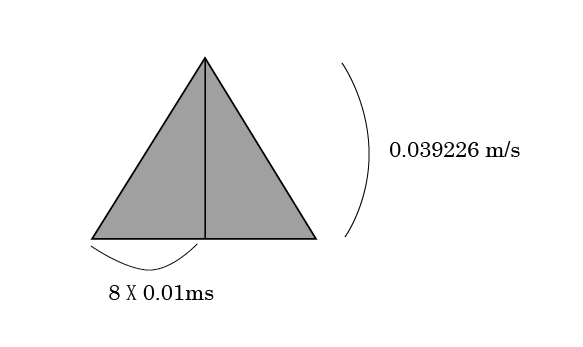
そうすると、移動した距離は、
0.08X2X0.039226/2=0.00313808(m)
すなわち、3.2ミリ移動したことになる。私が先に数ミリ動かしたと言ったが、ほぼその値に一致する。
ということは、この加速度センサーが捉えている加速度は、ノイズできなものはありながらも、なかなか、実態を反映しているということなのである。