前の記事で書いたロボットが倒れる、倒れない問題について、シミュレーション解を出すことができた。なお、計算に使ったJAVAの関数は、以下の論文の中に示しておいた。
（詳細は論文参照）
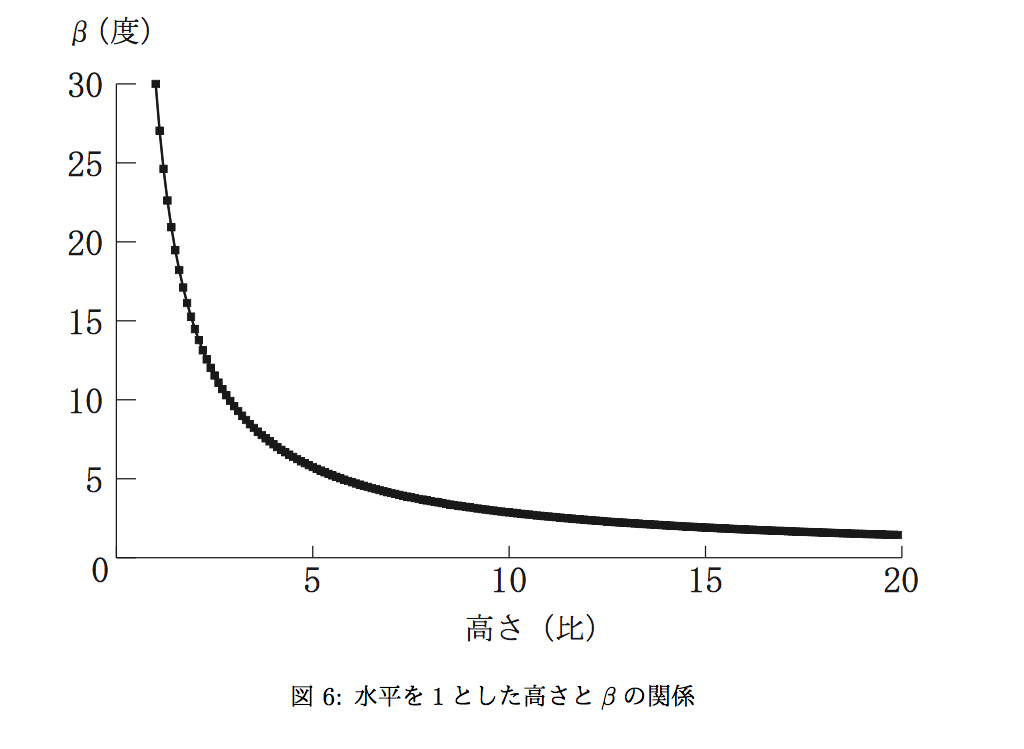この図で、横軸は、横の棒の長さを1としたときの高さである。縦軸が、転倒を回避するために、臨界点で止まる（再び位置エネルギーが元の値に戻る）ために必要な関節を固定化する角度である。ラディアンから度に変換している。
計算結果の誤差は、ここで解とみなした値のときで、高さの比が1のときが最も小さく0.0000000082である。高さの比がここで調べた中で最も大きい20.0のときに0.0000011608である。いずれもゼロに極めて近く、ほぼ解であると考えて間違いないだろう。刻み方をもっと細かくすれば、さらに誤差を小さくできることが予想される。ただ、高さが高くなるほど誤差は僅かながら大きくなっている。その理由は、高さが高いと、微妙なバランスが求められると考えても良いだろう。
その結果の特徴は、まず、理由はまだ正直わからないのだが、常にαとβは等しくなる。
高さが１のとき、すなわち、横棒と縦棒が同じとき、角度は29.99697622度、ほぼ30度だ。何か理由がありそうな角度である。αも同じになることは先に述べておいた。綺麗に90度を三等分する角度になっている。ただ、この角度は大きい。つまり、頂点で手を離して、30度傾くまで、自由な関節の回転を放置しておいて良いのだ。その後固定化すると、ギリギリ転倒を回避できる。高さが低いからである。
小さなロボットが転倒しにくい理由はここにある。
また、比率で見た高さが高くなると、最初は急速に関節を固定化するまでの角度が小さくなっている。その後は、少しずつ低下する。すなわち、高さが高くなればなるほど、転倒しないために関節を固定化しなければならないタイミングは早くなるのである。僅かに傾いたら、即固定化ということになっていく。
それでも、高さが10のときに、β=2.870976923度、ほぼ3度の余裕がある。3度傾いたら、関節を固定化しなければならないのである。高いと、微妙な調整が必要になる。
これだけでも面白い結果だが、人に応用するともっと興味深い。例えば、私の身長は182cmである。一方、足のくるぶしの関節から足のつま先までの長さは18cmくらいである。高さの比は、10.1である。
上の計算で、10.1の限界度、βは、2.843990611度である。つまり、足前に出したりせずに、動かさずに立った状態を維持するためには、2.8度、前に傾いたら筋肉を緊張させなければならないのである。
確かに、体を前にわずかに倒そうとすると筋肉を硬直させるが、この角度が、2.8度だよとこのシミュレーション結果は示している。もちろん、人間の体は質量が分布しているので、理論モデルで示したような質量の一点集中とは違っている。
一つ首をかしげることは、常にαとβが、ぴったり等しくなることである。数学モデルから、解析的に言えそうなのだが今の所わからない。
残された課題は、（１）頂点から倒れ始めて、関節が固定され、最終的に転倒の臨界角度に至るまでの時間を示すことである。確かに、高さが高いほど、関節を固定しなければならなくなるまでの角度は急速に小さくなっていく。しかし、そこに至る時間はどうなるかわからない。それを解析に出せないかを考えることである。また、その時間には、B点の質量が影響を与える可能性が高い。メトロノームが重りを上に持っていけばいくほど、スピードが遅くなることも考慮される。（２）実際にシステムを組んでシミュレーションして確かめることである。シミュレーションするための材料はほぼ整っている。加速度センサーも、サーボも、RaspberryPiから制御できるようになっているからである。