二足歩行目指して「足郎1号」(足しかないので、いや、足しか作る予定がない、笑)組み上げました。この段階ではまだ、膝関節をつけていないので、実用版ではなく、実験版です。「足郎2号」で、膝を持った普通の「足」にする予定。
足が前後していたり、微妙に開いていたりするので、まず、サーボ角度0で直立している状態をきちんと作ってから動かします。
予測していたより安定性が高い。前後に倒れる力と左右に揺れる力を利用してある貸そうと思っているので、あまり安定していてもいけないが、それはそれでいい。
サーボの反応速度が悪くなければ、二足歩行に持っていけるはず。
カテゴリー: ロボット製作
リード線作り
駆動の原理
基本的に、
(1)重心がかかっているときには、関節を固定させる。
(2)重心がかからず、関節が自由なときに、駆動させる。
(3)関節が固定化されている時の上板の加速度が意味を持つ。
フレームの作成
さしあたって「膝なし版」の二足歩行ロボットに向けて、アルミの枠組みを作成した。
昔見た、ブリキの廃材で作ったロボットの雰囲気。関節に駆動力がかからないので、遊びが大きく、ネジ穴が多少合わなくても問題なし。
今日中に、このフレームに、サーボモータ16個を取り付けて、ハード的なところを完成させたい。16個も(!)大丈夫かな(笑)
倒れこみとしての二足歩行
ロボットの現在の二足歩行が不自然なのは「倒れこみ」が基本になっていないからだ。
人は歩く動きは、ただ前に倒れ続けているだけなのだ。それは、人工衛星が地球に落下し続けているのと似ているかもしれない。倒れるときに、大きな力は必要がない。だから人も、歩くことに大きなエネルギーを使わない。前方に倒れかかると片足を前に出す、新しい足が低になって回転する。さらにその回転が前に倒れこむ。別の足を出す。ただそれの繰り返しである。
倒れる!おっとっと、足を前に出そう、である。
そのとき、ただ、体が左右に揺れる。これは、倒れない程度に揺れる必要がある。なぜなら、倒れこみの時、足を前に出す必要があるが、その足には重心がかかっていてはならないからである。
従って「倒れ込まない揺れと」「倒れ込んでしまう揺れ」の二つを繰り出して、人は歩いていく。
現在のロボットは、関節の角度を変えながら歩いていく。倒れこみはない。倒れこみなどすると、本当に倒れてしまう。
逆振り子ロボットの転倒データ
逆振り子ロボットに、いろいろな転倒をさせてみた。あるいは、転倒の回避を試みた。数え切れないほどやったが、その一部を書いておきたい。

逆振り子ロボットアイコメ01の雄姿(笑)は左のようなものだ。写真では、左右方向にだけ倒れるように作ってある。足先に向けて、2台のサーボのワイヤーが張ってあるので、これを張ったり緩めたりして転倒させたり、転倒を制御させたりしている。
写真は、サーボ角度をほぼニュートラルにちかい位置にして直立させている。
サーボを緩めて、自然転倒させた時の3軸加速度センサーが捉えるデータを示しておこう。
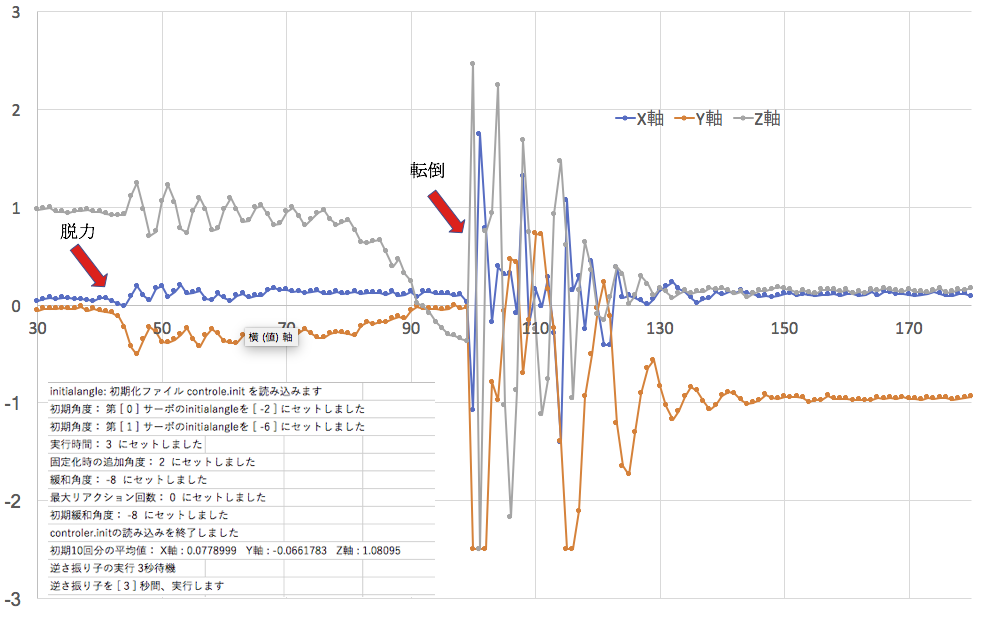
横軸の目盛りは10ミリ秒単位で、センサーから撮ってきたデータの番号である。縦軸は上から順に、Z、X、Y軸の加速度センサーのデータである。
Z軸は、垂直方向であるが、サーボの脱力によって上下の微妙な揺れが生じるが、倒れるに従ってそれは減衰している。青がX軸だが、倒れないようになっている方向のため、微妙な揺れだけにとどまっている。一番下のY軸のデータが、倒れる方向のものだ。ただ、ゼロから、一挙に(回転方向である負の方向に)上昇するが、倒れるに従ってまたゼロに戻っていっている。回転に従ってこの方向の動きがなくなるからである。倒れた瞬間に、加速度センサーはパニックになる。
このパニック状態は、ロボットが一番不快な状態になっていると考えれば良い。これは、のちに、ロボットに運動を学習させるときに、不快感のシグナルとして使いたいと思っている。
衝撃が治ると、Y軸が垂直になっているので、1g(gは重力加速度)になって、他はほぼゼロになっている。わずかの傾きがあるくらいだ。
次に、転倒をロボット自身んが検知した瞬間(0.1gの変化)、転倒する反対側のサーボを、角度を縮める形で固定した。すなわち、逆方向に揺り戻そうと動かした時の反応は、次のようになる。
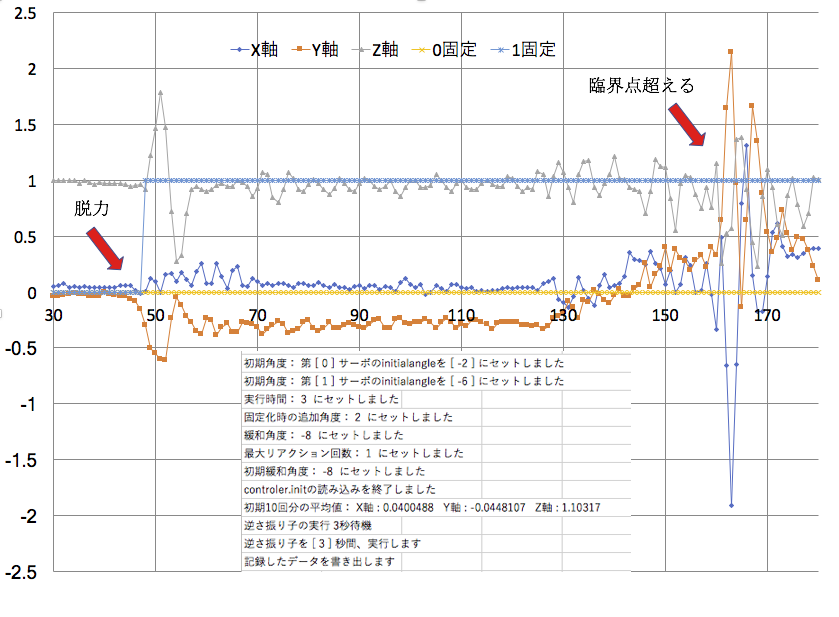 まず、Z軸が、脱力と片側固定化の、一瞬の大きな揺れの後、1gを維持している。先の完全転倒の場合と比べて、水平状態がほぼ維持されていることを意味している。それでもわずかに左に傾いていることは、Y軸の動きによって知ることができる。それが一見安定しているようだが、脱力から0.8秒後に反対側に向かっての回転が発生して、矢印のところで臨界点を超える。この臨界点を超えるというのは、データからの判断ではなく、ロボットを見ていた私が、これは、ほっておけば倒れると判断したところで、私がその時点でロボットを支えた。
まず、Z軸が、脱力と片側固定化の、一瞬の大きな揺れの後、1gを維持している。先の完全転倒の場合と比べて、水平状態がほぼ維持されていることを意味している。それでもわずかに左に傾いていることは、Y軸の動きによって知ることができる。それが一見安定しているようだが、脱力から0.8秒後に反対側に向かっての回転が発生して、矢印のところで臨界点を超える。この臨界点を超えるというのは、データからの判断ではなく、ロボットを見ていた私が、これは、ほっておけば倒れると判断したところで、私がその時点でロボットを支えた。
最初の転倒方向への完全転倒は避けれたのだが、逆のサーボが引き戻したことによって、逆側に倒れてしまう事態になったというわけである。
1関節ロボット上の加速度センサーデータ
(以下の記事の元になっているのは、この論文)
1関節ロボット、アイコメ0.1(外形はこちら)上におかれている3軸加速度センサーが転倒に対してどのように反応するかを調べてみた。
正直驚いた。ロボットに載せずに、机の上で動かしたりのシミュレーションはすでに行っていて、その結果も示しているが、その結果とは大きく違っている。
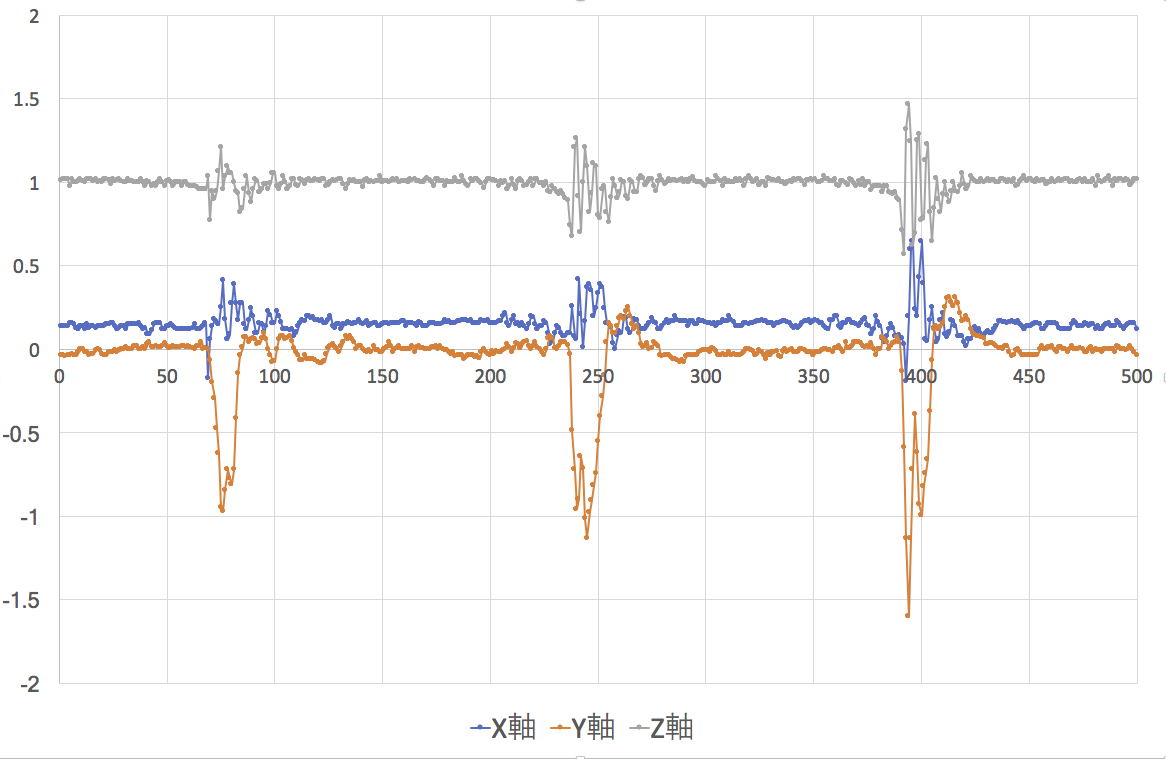 垂直に立てた状態から、手を離して、5度か10度自由に傾かせて、手で止めてまた垂直に戻すというのを3回やったデータである。止めたところは、およそ、ここで関節を固定させたらいいなと、私が判断した場所である。
垂直に立てた状態から、手を離して、5度か10度自由に傾かせて、手で止めてまた垂直に戻すというのを3回やったデータである。止めたところは、およそ、ここで関節を固定させたらいいなと、私が判断した場所である。
(1)重力の誤差が小さい。Z(縦)方向のg(重力加速度)は1で、他はゼロが理論的に予想されるところだ。ほぼ、そんな感じだ。Y軸は、私がほぼ水平(すなわち棒が垂直に立っている)と思われるように調整しているが、前後の軸(X軸)は、丁寧に調整していないのでわずかにずれている。
(2)一度の揺れを感度良く捉え、たくさんのデータを輩出している。前の結果と比べてもらえば一目瞭然だ。サーボによる調整のトリガを出す上で、とてもわかりやすい。
ここで、理論的に予測される、臨界角度を調べてみよう。アイコメ01は10センチの横棒の中央から33センチの高さ(コンピュータが置かれているアルミ板までの高さ使う)だから、その比は6.6である。この場合の臨界角βは、ラディアンで0.075869、角度で4.346973501度であることがわかっている(この論文参照)。
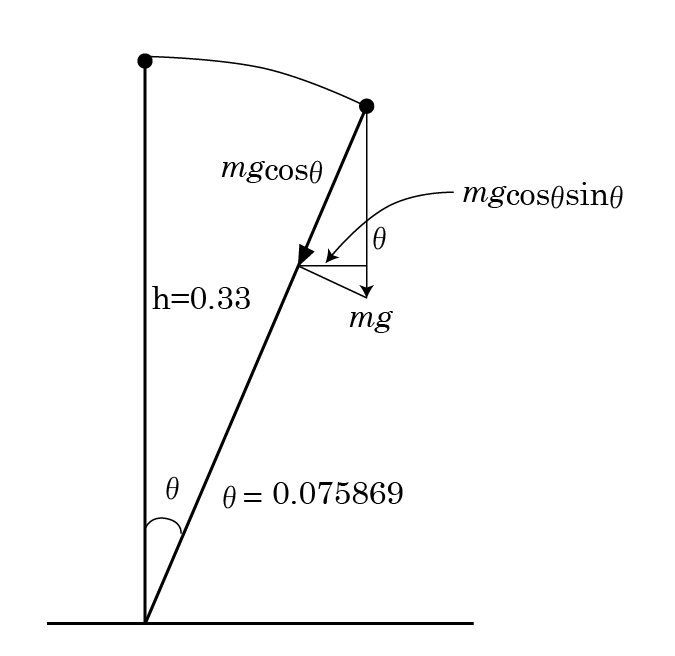
すると、左の図からわかるように、Y軸方向の加速度は、sinθcosθであるから、重力加速度のsinθcosθになったときが垂直からの角度がθになったときであることがわかる。このθに0.075869を入れると、上記の値は、0.001324162となる。つまり、Y軸方向の加速度が絶対値で、0.001324162ときである。
もし、この理論値が正しければ、極めて初期の段階で、関節の固定が必要となることを意味している。
サーボモータに、こんなに微妙なコントロールは不可能であるから、実際上は、センサーが倒れ始めているデータを出し始めた途端、関節を固定化するようにサーボの角度を与えることが必要になる。
1関節ロボットによる逆振り子理論の検証
(以下の記事の元になっているのは、この論文である)
早朝から、アルミの板と棒を切ったり穴開けたりしながら、この間議論してきた理論を実証すべく、自由な関節を1個だけ持ったロボットを作った。たくさんのボルトやナットを使ったが、一時期、電子工作に凝っていたので、その時のものでほとんど間に合わせた。
「冷蔵庫にあるものでラーメンを作った」という感じのロボットだ。
いや、「これはロボットではない」と言われればあえて否定しないが、自分では、私が自分で作った最初のロボットの筐体だと思っている。脳はあるが、まだ知恵は何も入っていない。あえて名前をつければ、AiComedian ver.0.1 である。アイコメと呼ぼうか。
 アルミの縦棒が机についているあたりに、アルミの横棒があり、それらをつないでいるのが横方向にだけ自由に回転する関節、ジョイントである。
アルミの縦棒が机についているあたりに、アルミの横棒があり、それらをつないでいるのが横方向にだけ自由に回転する関節、ジョイントである。
横棒には、前後に倒れないように4ミリのアルミ棒が左右に二本つけられている。だから、この縦棒は、左右にしか動かないのである。
ただし、今こうして立っているのは、上部に二つのサーボモータがついていて、下の横棒との間に0.3ミリのステンレス線が張ってあるからである。
さらにその上には、コンピュータ( RaspberryPi)と3軸加速度センサー、I2Cによるサーボコントローラを乗せたアルミの板がある。
サーボは、水平角度を0度として運用しているが、およそであって、今の状態は、手前のサーボ(1番)がサーボの角度で0度、向かいのサーボ(0番)がサーボの角度で+3度でほぼ釣り合った状態になっている。サーボの角度を下向きに変化させると、縦棒は勢いよく倒れる。
C++で加速度センサーとサーボをコントロールするクラスを、それぞれに作ってあるので、センサーの検出した傾きから、サーボをコントロールして、逆さ振り子の状態を実際に創り出したいと思っている。
ことの成否は、転倒開始時に、加速度センサーがどんなデータを送ってくるかにかかっている。
加速度センサーの精度
(以下の記事の元になっているのは、この論文)
ロボットの転倒に関する議論をしてきたが、逆振り子で転倒を回避する場合でも、自らの傾き、ないしは揺らぎを捉えることが不可欠である。ここでは、KXSD9-2050という750円のセンサーを使っているので、どこまで精度が出るのかがいたって不安である。
そこで、より詳細に調べてみた。
KXSD9-2050については、sensitivityを819counts/g (g: 重力加速度 = 9.80665 m / s2)に変更したことを除いて、初期設定を採用している。
10ミリ秒に一つのデータを取る計算で、500個のデータを取った。その間に、センサー(RaspberryPiに固定している)を6回だけ、数ミリずらせる速度をY軸方向に与えた。そのうちの50個目から200個目までのデータを図で表したものが以下の画像である。
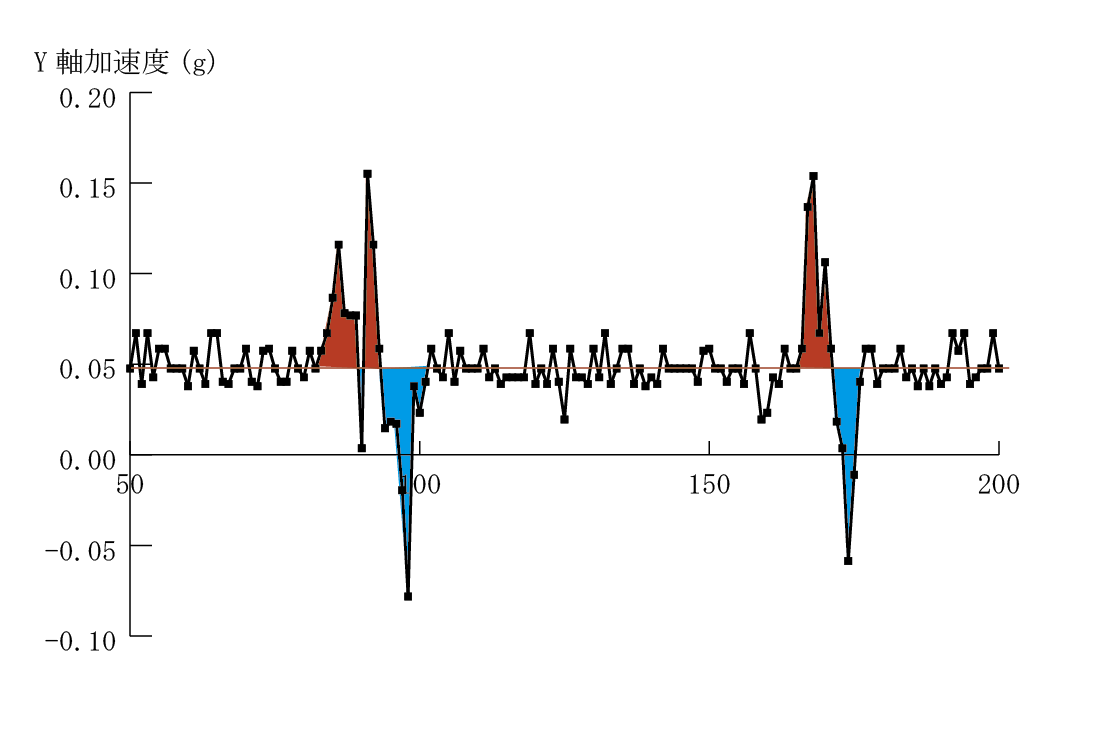 Y軸だけをみている。縦軸のgはY軸方向の重力加速度である。水平方向であるから0でなければならないが、0.05となっているのは、多少Y軸が傾いていることからくるのか、私の家が傾いているのか、机が傾いているのか、そんなところだろう。ホワイトノイズとして処理する。
Y軸だけをみている。縦軸のgはY軸方向の重力加速度である。水平方向であるから0でなければならないが、0.05となっているのは、多少Y軸が傾いていることからくるのか、私の家が傾いているのか、机が傾いているのか、そんなところだろう。ホワイトノイズとして処理する。
数ミリ動かしたことによる影響は、赤と青で色ぬりされた部分に現れている。赤から始まっているのは、Y軸のプラスの方向に加速度が与えられ、マイナスになっているのは、速度が低下して、ほぼ再び止まったことを表している。止まったということは、赤の面積と青の面積がほぼ等しいことを表す。
実際移動した距離は加速度がプラスから始まっているので、Y軸方向に移動してどこかで止まったということで、それまでのプラスの距離になる。
指で数ミリ動かしただけで、これだけのものがとらえられることは、この安物のセンサーも結構使える可能性があることを示している。
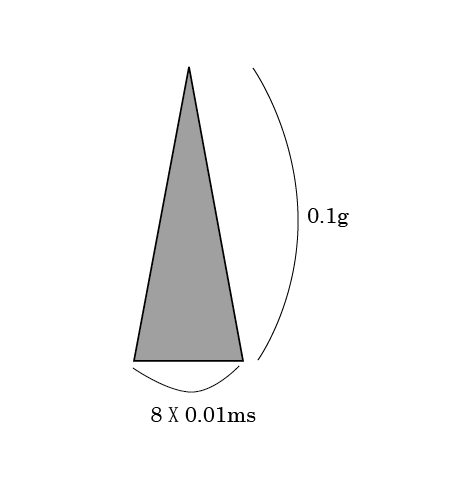 今、赤と青の部分が単純な三角形だったとしよう。横幅が8目盛、高さが0.1gくらいになる。この時、最高速度は、
今、赤と青の部分が単純な三角形だったとしよう。横幅が8目盛、高さが0.1gくらいになる。この時、最高速度は、
80(ms)X0.1(g)X(1/2)=0.08X0.1X0.5X9.80665=0.039226(m/s)
およそ1秒間に4センチ動くくらいの速度が最高速度だったということになる。
それから速度が0になるまで同じくらいの時間がかかったとしよう。簡単化のために、全て、三角形で捉えよう。(実際は曲線)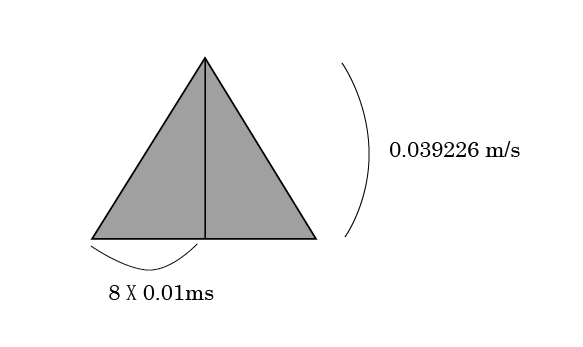
そうすると、移動した距離は、
0.08X2X0.039226/2=0.00313808(m)
すなわち、3.2ミリ移動したことになる。私が先に数ミリ動かしたと言ったが、ほぼその値に一致する。
ということは、この加速度センサーが捉えている加速度は、ノイズできなものはありながらも、なかなか、実態を反映しているということなのである。
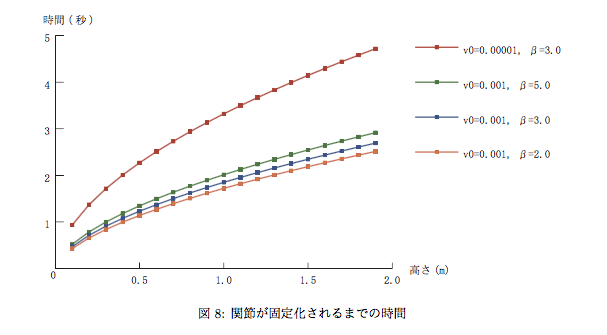
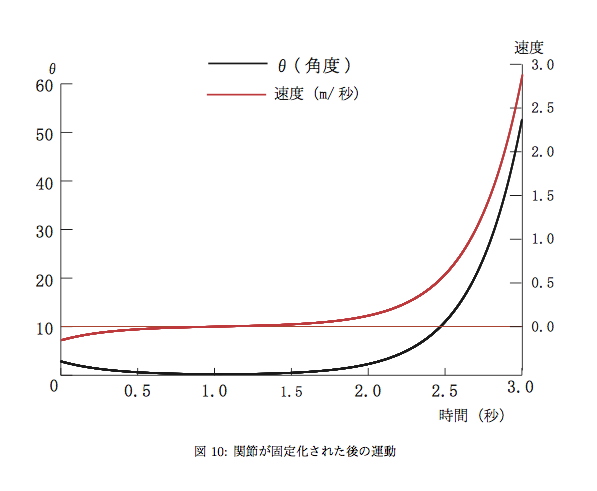
時間を入れたシミュレーション
ロボットの転倒とその回避に関わる分析で、これまでは明示的に時間が入らなかった。そこで、ロボットの転倒と回復に関する運動方程式を求めてシミュレーションしてみた。
結果の詳細は論文参照