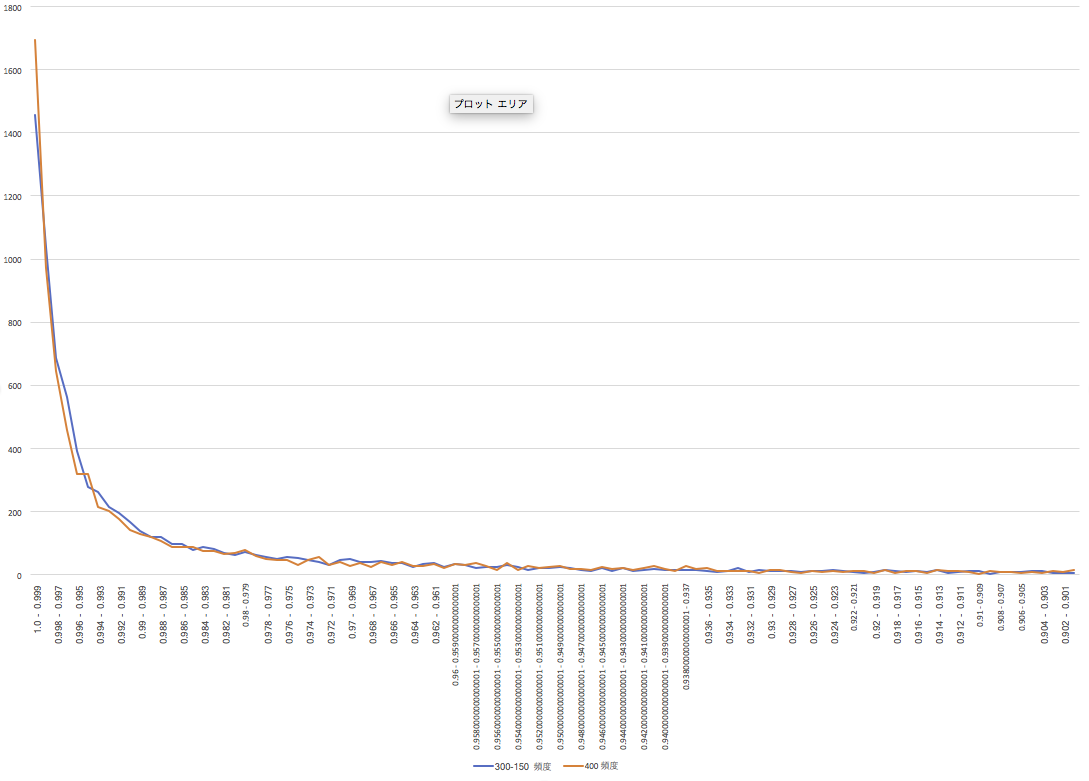
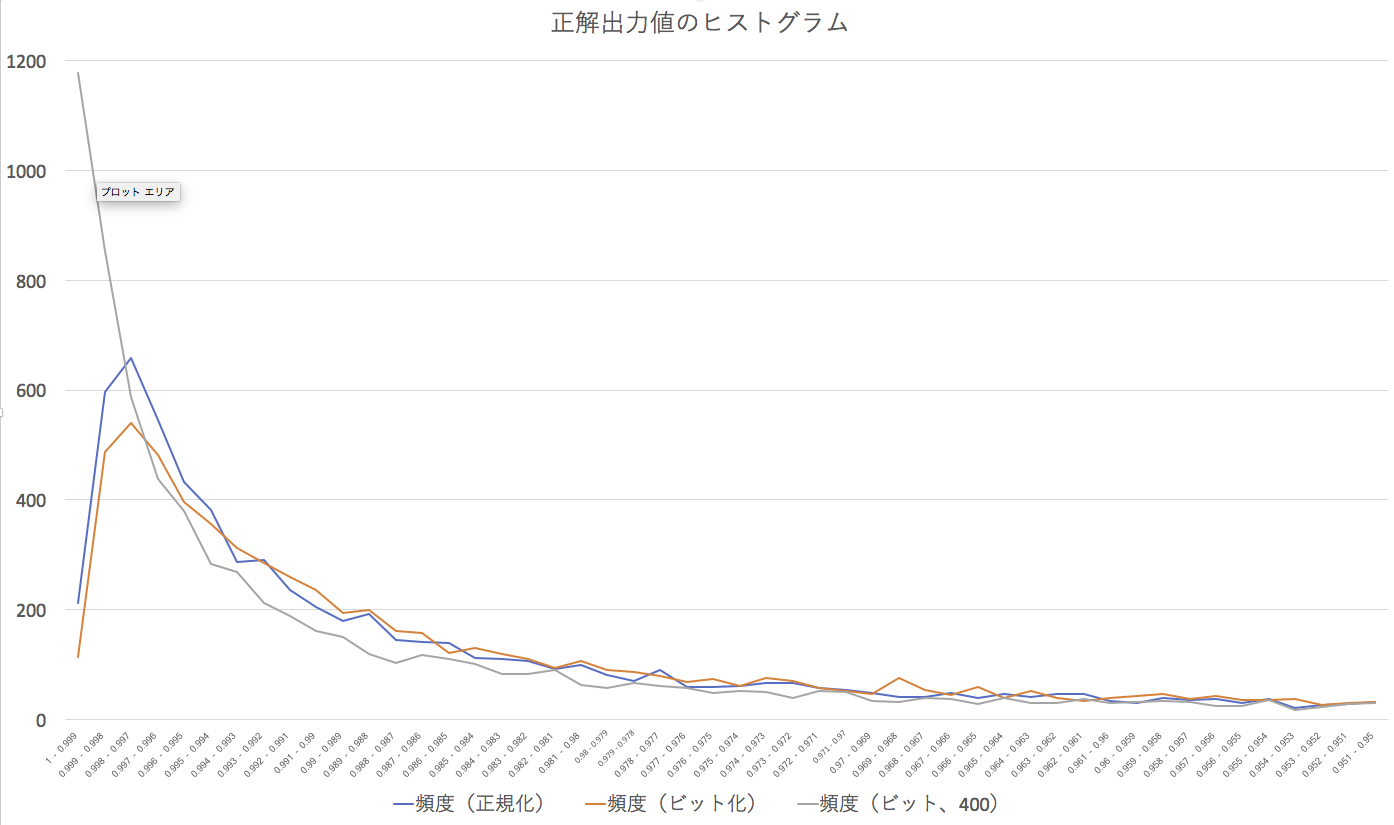
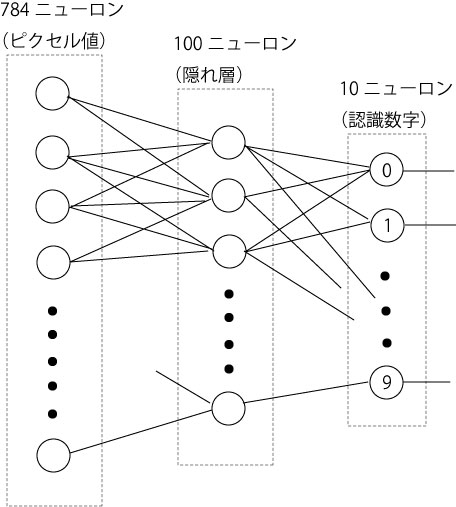
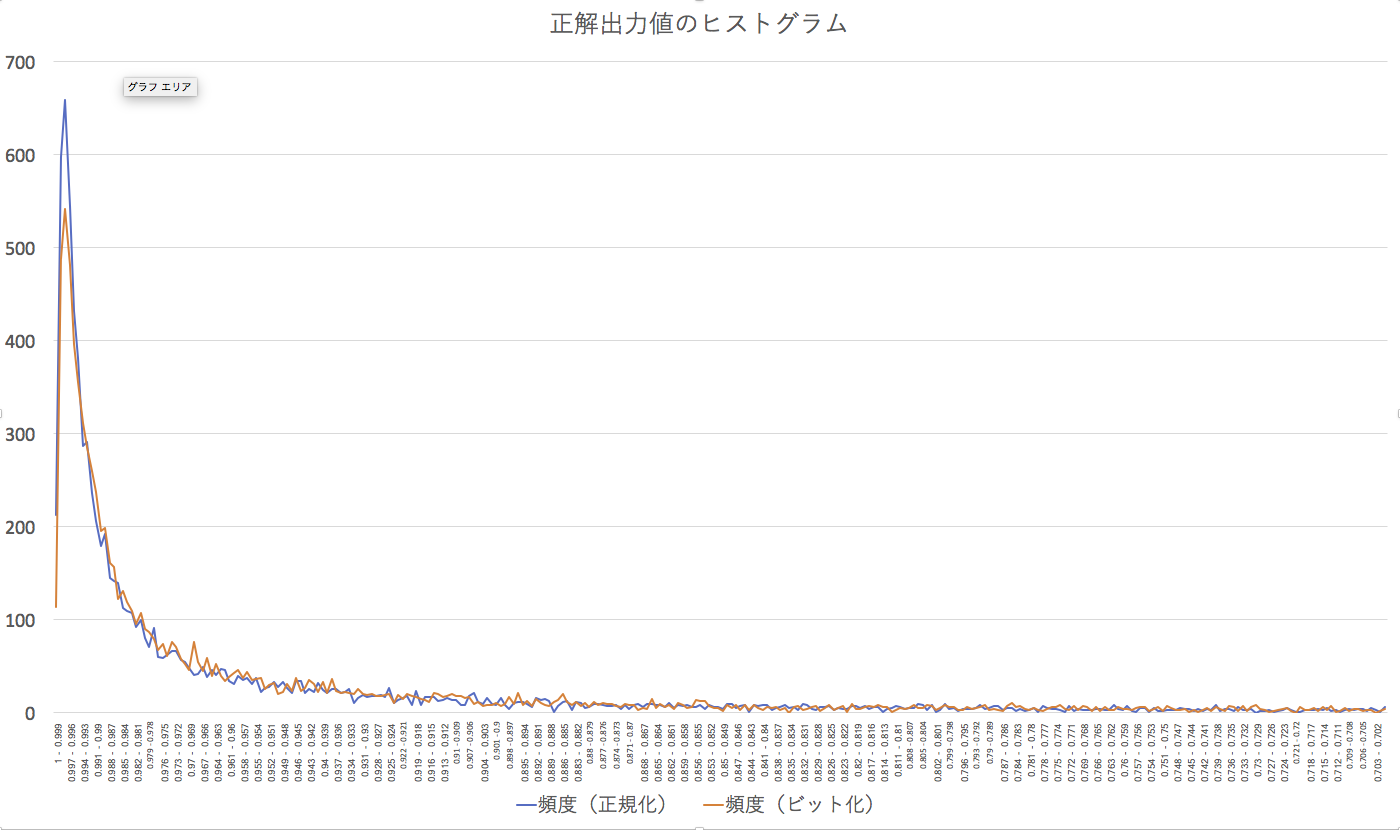
プログラム本体こちら https://github.com/toyowa/jautoencoder
ここでは、JDeeplearningの個々のクラスの説明をしておく。クラス内の主なメソッド(メンバー関数)の説明をする。
<JDeepLearningクラス>
メインクラスだ。mainのスタティック関数が入っている。
public static void main(String[] argv)
冒頭で、自分、JDeepLearningクラスのインスタンスdplを作成する。
何よりも、プログラムを開始する関数がだ、ひたすらオプションの処理をしている。オプション処理後に、
dpl.dataProc.setTrainData(dpl.dataFileName);
で、データを読み込んでいる。
そして、オートエンコーダーなら
dpl.execAutoencoder(topology);
普通のニューラルネットならば、
dpl.execNeuralnet(topology);
という、自分のクラスのメソドを呼び出している。
void execAutoencoder(int[] topology)
オートエンコーダーの実行関数である。(1)で説明したように、隠れ層ごとのサブネットワークを形成する。形成してから、
execNeuralnet(topology)
を呼び出して、バックプロパゲーションでウェイトを作成し、隠れ層ごとにこれを繰り返して、最後は最終層へのウェイトをランダムに作成した、これまでのウェイトと合同させて、ファインチューニングのオリジナルなネットワークを形成して、
execNeuralnet(topology);
に渡している。
ここで、
static double[][][] reserved_weights;
というウェイトを保持するスタティックな3次元配列reserved_weightsが重要な役割を果たしている。第1次元は、レイヤー番号で、0番が第1レイヤーであることに注意してほしい。0番レイヤーには入力ウェイトがないから無駄にならないようにそうしている。第2次元は、そのレイヤーのニューロン番号を指定し、第3次元は、その中のウェイト番号である。配列をメモリー状にインスタンス化する時、ウェイト数は、ニューロンごと(レイーヤー数に基づいて)に異なっているのだが、各レイヤーのニューロン数の最大数で作ることにしている。そして、この配列にデータがあると、Neuronクラスがインスタンス化されるときに、ウェイトの初期値をランダムな数ではなく、ここにある値で初期化されるように作られている。
だから、実行オプションの-weightsでウェイト配列が指定されると、そのウェイトがこのスタティックな、reserved_weightsに保持され、自動的にNeuronクラスのインスタンス化の時にセットされるのだ。
void execNeuralnet(int[] topology)
ニューラルネットワークを起動する。基本、順方向に出力を作る作業と逆方向に、バックプロパゲーションを実行するという、二つの作業をやっている。テストの時は、順方向の作業しかしない。
冒頭で、関数引数のtopologyに基づいて、ニューラルネットワークを作り上げる。具体的には、のちに説明するNetクラスを作り、その中に、Layerクラスで、レイヤーを作り、さらにその中で、Neuronクラスでニューロンを作成するという入れ子構造でネットワークを作成している。つまり、Netのインスタンスの中にレイヤーの数だけLayerインスタンスを作り、各レイヤーの中に必要なニューロン数のNeuronインスタンスを作るわけである。そのかくNeuronインスタンスがウェイトを保持している。
オートエンコーダーで呼び出される場合は、出力の教師学習データが、入力データと同じなので、その辺りの場合分けがされている。
<Netクラス>
Netクラスは、ネットワークの構造と、内部機能を実現するメソッドを保持している。
メンバー変数は、
double [] outputs;
Layer [] layers;
int [] topology;
double adjusting;
で、最初が、出力値を保存している変数、次が、ネットワーク内のレイヤーを保持している変数、topologyは、Netクラスがインスタンス化される過程で与えられるネットワーク構造を保持している、最後のadjustingがバックプロパゲーションでウェイトを調整する係数なのだが、ほとんど、0.15のままにしていて、変更の気持ちがなかったので、このクラスのコンストラクタ内で値を与えて終わりにしていたが、これも実行時オプションで指定できるようにすべきだ。次の改訂ではそうしようと思う。
String makeAutoencoderData(Data dataProc)
オートエンコーダーで次の隠れ層のウェイト形成のための入力データを作成する。つまり、前の隠れ層の時の第1層のウェイトを使ってその前の入力データから出力データを作成するわけである。
tmpout_時間.txt
というファイル名にして保存している。
String printAllWeights(int iteration, String dataFileName)
ネットワークの全ウェイトを出力する。ファイル名は、
weight_時間.wgt
である。ここのレイヤーの出力、ニューロンの出力はそれぞれのクラスに下請けに出す。
void adjustingPreLayerWeightsOut(int layerNo)
ニューロンは、そのニューロンへの入力側のニューロンからの結合ウェイトと、出力側へのウェイトの両方を保持することになっている。なぜそうしているのかといえば、順方向への出力値の計算は、入力側のウェイトデータが必要で、誤差逆伝搬の計算においては、出力側のウェイトが必要だからである。ニューロンに関わる計算はニューロンクラスのメソッドで行われる。ただ、この入力側ウェイトと出力側ウェイトは、あるニューロンの出力ウェイトは次のレイヤーのニューロンの入力ウェイトになるので、両者は同じものでなければならない。それは、ここのニューロン内の計算でもダメで、レイヤーもまたがるので、このNetクラス内のメソドで整合性を取るようにしているのだ。
これを書いている時に改めても直したら、余計な場所で使われているの気づいて直した(このメモのおかげでバグフィックスできた!)。実質計算に影響はないが、微妙に速さが変わったかもしれない。試してみたが、計算結果には影響なく、速さの変化はわからない。
ただ、一つ大事なことを書いておくと、この、Deltaに基づくウェイトの訂正は、ネットワークの全てのDeltaを計算し終えてからにしなければならない。従ってその後に、ウェイトの整合性は図られる。
void getForwardOutput(double [] initVal)
ウェイトに基づく、順方向の出力値の計算をネットワーク全体で実施する。レイヤー、ニューロンに実際の計算は下請けさせている。
void execBackpropagation(double [] deltaE)
誤差逆伝搬の計算。実際の計算は、下請けに任せている。
<Layerクラス>
メンバー変数は以下の通りである。
Neuron[] neurons;
double[] layerOutput;
double[] layerDelta;
double adjusting;
int layerNo;
レイヤークラスは、ネットワーククラスとニューロンクラスの間を取り持っている感じで、大事な計算はあまりない。省略。
<Neuronクラス>
ニューロンクラスのメンバー変数は、
int neuronNo;
int layerNo;
double adjusting;
boolean inputNeuron = false;
boolean outputNeuron = false;
double [] weightsIn;
double [] weightsOut;
double [] prev_output;
double output;
double delta;
double value;
である。
コンストラクタで、ウェイトを組み込むのが大事な作業だ。JDeepLearningのクラスのところでで書いたが
JDeepLearning.reserved_weightsが入っていれば、それをウェイトに組み込み、なければ乱数で作成する。
乱数で作成する時に、単に0から1までの間の数字にすると、出力値が大きくなりすぎてダメになるので、その乱数を入力側のウェイト数で割って正規化する。これで、改善された。
weightsIn[i] = Math.random() / (double) inputNum;
となっている。
void getNeuronDelta(double[] prev_delta)
バックプロパゲーションでいうDelta値をこのニューロンについて計算する。入力値の合計valueで、シグモイド関数の微分値の値を計算する必要があるのだが、
delta = 0.0;
for (int i = 0; i < prev_delta.length; i++) {
//前の層のデルタに、そのニューロンとのウェイトをかけたもの
delta += prev_delta[i] * weightsOut[i];
}
double ev = Math.exp(-value);
delta = delta * (ev / ((1 + ev) * (1 + ev)));
で、計算している。
void getNeuronOutput(double [] prev_output)
順方向の計算を行う関数だ。
<Dataクラス>
ファイルの入出力を担う関数だが、特別なことはないので省略する。データがどのように保存され読み込まれるのかが見れば分かるはずである。